List of Procedural Texture Clamping, Noise and Misc Functions
See Also: Class Texmap, Class AColor, Class Color, Class Point2, Class Point3.
The following functions are available for use in the creation of procedural textures. These are based on the code provided in the book:
Kenton Musgrave, Darwyn Peachey, Ken Perlin, Steven Worley, Texturing and Modeling A Procedural Approach (Cambridge, MA: Academic Press, Inc., 1994). ISBN: 0-12-228760-6.
Consult this book for additional insight into the use of these functions.
Prototype:
float boxstep(float a, float b, float x);
Remarks:
This function returns 0 if x is less than a, a linear interpolation between 0 and 1 if x is greater than or equal to a and less than or equal to b, and 1 if x is greater than b. This function is a smoother version of step() using a linear ramp. The function boxstep() is defined like this:
float boxstep(float a, float b, float x) {
return clamp((x-a)/(b-a),0.0f, 1.0f);
}
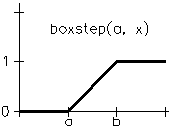
The boxstep() function.
For comparison, note that step() returns values of 0 when x is less than a and 1 when x is greater than or equal to a. This function is not part of the SDK but step() is defined like this:
float step(float a, float x) {
return (float)(x >= a);
}
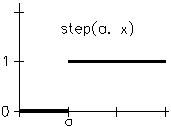
The step() function.
Parameters:
float a
The limit for the x value where the function will return 0.
float b
The limit for the x value where the function will return 1.
float x
A floating point value.
Prototype:
float smoothstep(float a, float b, float x);
Remarks:
This function is similar to step(), but instead of a sharp transition from 0 to 1 at a specified threshold, it makes a gradual transition from 0 to 1 beginning at threshold a and ending at threshold b. To do this, this function uses a cubic function whose slope is 0 at a and b and whose value is 0 at a and 1 at b. This function thus provides a still smoother version of step() using a cubic spline. The smoothstep() function is used (instead of step()) in many procedural textures because sharp transitions often result in artifacts.
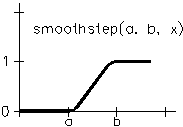
The smoothstep() function.
Parameters:
float a
The limit for the x value where the function will return 0.
float b
The limit for the x value where the function will return 1.
float x
A floating point value.
Prototype:
float clamp(float x, float a, float b);
Remarks:
This function returns a when x is less than a, the value of x when x is between a and b, and the value b when x is greater than b. The function clamp() is defined as follows:
float clamp( float x, float a, float b) {
return (x < a ? a : (x > b ? b : x));
}
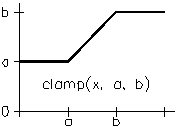
The clamp() function.
Parameters:
float x
A floating point value.
float a
A floating point value.
float b
A floating point value.
Prototype:
float mod(float x, float m);
Remarks:
This function returns x Mod m and handles negatives correctly. The standard math functions fmod() and fmodf() return negative results if the fist operand, x, is negative. This function will return the positive remainder when dividing x by m.
Parameters:
float x
A floating point value.
float m
A floating point value.
Prototype:
int mod(int x, int m);
Remarks:
This function returns x Mod m and handles negatives correctly.
This function returns x Mod m and handles negatives correctly. The standard C remainder operator % return negative results if the fist operand, x, is negative. This function will return the positive remainder when dividing x by m.
Parameters:
int x
An integer value.
int m
An integer value.
Prototype:
float sramp(float x, float a, float b, float d);
Remarks:
This function makes a sort of straight segment S curve.
sramp() is a for x less than a-d and b for x greater than b+d.
for a+d < x < b-d sramp(x) = x
for a-d < x < a+d sramp() makes a smooth transition (parabolic) from sramp' = 0 to sramp' = 1
for b-d < x < b+d sramp() makes a smooth transition (parabolic) from sramp' = 1 to sramp' = 0
Parameters:
float x
A floating point value.
float a
A floating point value.
float b
A floating point value.
float d
A floating point value.
Prototype:
float threshold(float x, float a, float b);
Remarks:
This function returns 0 if x is less than a, 1 if x is greater than b, otherwise it returns x.
Parameters:
float x
A floating point value.
float a
A floating point value.
float b
A floating point value.
Prototype:
float bias(float a, float b);
Remarks:
This function performs a mapping across the unit interval [0, 1] where the result is within the unit interval. That is, if b is within the interval 0 to 1, the result of bias() is within the interval 0 to 1. This function is defined such that bias(a, 0.5)=a. The function looks like:
float bias(float a, float b) {
return (float)pow(a, log(b) / log(0.5f));
}
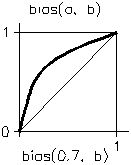
The bias() function.
Parameters:
float a
The parameter that determines the shape of the mapping.
float b
A floating point value.
Prototype:
float gain(float a, float b);
Remarks:
This function performs a mapping across the unit interval [0, 1] where the result is within the unit interval. That is, if b is within the interval 0 to 1, the result of gain() is within the interval 0 to 1. This function is defined such that gain(a, 0.5)=a. Above and below 0.5, this function consists of two scaled down bias() curves forming an S-shaped curve. The function looks like:
float gain(float a, float b)
{
float p = (float)log(1.0f - b) / (float)log(0.5f);
if (a < .001f)
return 0.f;
else if (a > .999f)
return 1.0f;
if (a < 0.5f)
return (float)pow(2 * a, p) / 2;
else
return 1.0f - (float)pow(2.0 * (1. - a), (double)p) / 2;
}
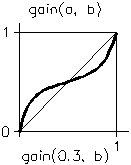
The gain() function.
Parameters:
float a
The parameter that determines the shape of the mapping.
float b
A floating point value.
The following are noise functions over 1, 2, and 3 dimensions:
These are all simply noise functions of different dimension. They return values in the range [-1,1].
Prototype:
float noise1(float arg);
Remarks:
This function is an approximation of white noise blurred to dampen frequencies beyond some value. The return value is in the range [-1, 1].
Parameters:
float arg
A floating point value.
Prototype:
float noise2(Point2 p);
Remarks:
This function is an approximation of white noise blurred to dampen frequencies beyond some value. The return value is in the range [-1, 1].
Parameters:
Point2 p
A Point2 value.
Prototype:
float noise3(Point3 p);
Remarks:
This is a noise function over R3 -- implemented by a pseudo-random tricubic spline. This function is an approximation of white noise blurred to dampen frequencies beyond some value. The return value is in the range [-1, 1].
Parameters:
Point3 p
A Point3 value.
Prototype:
float noise4(Point3 p, float time);
Remarks:
This function is an approximation of white noise blurred to dampen frequencies beyond some value. The return value is in the range [-1, 1].
Parameters:
Point3 p
A Point3 value.
float time
A floating point value.
Prototype:
float noise3DS(Point3 p);
Remarks:
This is 3DStudio's Noise function: its only slightly different from noise3() scaled up by factor of 1.65 and clamped to -1,+1.
The following #define is also available:
#define NOISE(p) ((1.0f+noise3DS(p))*.5f)
Macro to map the value returned from the noise3DS() function into interval [0,1].
Parameters:
Point3 p
A Point3 value.
Prototype:
float turbulence(Point3& p, float freq);
Remarks:
This turbulence function is a simple fractal generating loop built on top of the noise function. It is used to make marble, clouds, explosions, etc. It returns a value in the range [0, 1].
Parameters:
Point3& p
The input point.
float freq
A floating point frequency.
Prototype:
int Perm(int v);
Remarks:
This function simply uses v as a lookup into a table to return a different number. It only uses the low 9 bits of the number (0-512) and returns a number in that range.
Parameters:
int v
An integer value.
Prototype:
float fBm1(float point, float H, float lacunarity, float octaves);
Remarks:
This function is a fractional Brownian motion fractal (or fBm for short) that returns a floating point value. This version of the fBm is said to be "homogeneous" (the same everywhere) and "isotropic" (the same in all directions).
Parameters:
float point
The function is evaluated at this value.
float H
The fractal increment parameter. When H = 1, the function is relatively smooth; as H goes to 0, the function approaches white noise.
float lacunarity
The gap between successive frequencies. This is usually set to 2.0.
float octaves
The number of frequencies in the function.
Prototype:
float fBm1(Point2 point, float H, float lacunarity, float octaves);
Remarks:
This function is a fractional Brownian motion fractal (or fBm for short) that returns a floating point value.
Parameters:
Point2 point
The function is evaluated at this point.
float H
The fractal increment parameter. When H = 1, the function is relatively smooth; as H goes to 0, the function approaches white noise.
float lacunarity
The gap between successive frequencies. This is usually set to 2.0.
float octaves
The number of frequencies in the function.
Prototype:
float fBm1(Point3 point, float H, float lacunarity, float octaves);
Remarks:
This function is a fractional Brownian motion fractal (or fBm for short) that returns a floating point value.
Parameters:
Point3 point
The function is evaluated at this point.
float H
The fractal increment parameter. When H = 1, the function is relatively smooth; as H goes to 0, the function approaches white noise.
float lacunarity
The gap between successive frequencies. This is usually set to 2.0.
float octaves
The number of frequencies in the function.
Prototype:
float spline(float x, int nknots, float *knot);
Remarks:
This function is used to map a number into another number. The function is a one-dimensional Catmull-Rom interpolating spline through a set of knot values. The parameter of the spline is a floating point value. If x is 0, the result is the second knot value. If x is 1, the result is the final knot value. For values between 0 and 1, the value interpolates smoothly between the values of the knots from the second knot to the second to last knot. The first and last knot values determine the derivatives of the spline at the endpoint.
The spline () function.
Parameters:
float x
A floating point value.
int nknots
The number of knots. Because the spline is a cubic polynomial there must be at least four knots.
float *knot
An array of floating point knot values.
Prototype:
Color color_spline(float x, int nknots, Color *knot);
Remarks:
This function is used to map a number into a color. The function is a one-dimensional Catmull-Rom interpolating spline through a set of knot values. The parameter of the spline is a floating point value. If x is 0, the result is the second knot value. If x is 1, the result is the final knot value. For values between 0 and 1, the value interpolates smoothly between the values of the knots from the second knot to the second to last knot. The first and last knot values determine the derivatives of the spline at the endpoint.
Parameters:
float x
A floating point value.
int nknots
The number of knots. Because the spline is a cubic polynomial there must be at least four knots.
Color *knot
An array of Color knot values.
Prototype:
inline int FLOOR(float x);
Remarks:
This function provides a faster version of the standard C function floor(). It returns a floating-point value representing the largest integer that is less than or equal to x.
Parameters:
float x
A floating point value.
Prototype:
inline float frac(float x)
Remarks:
This function returns the fraction (non-integer) part of the value passed. This is defined as:
{ return x - (float)FLOOR(x); }
Parameters:
float x
The value whose fractional portion is to be returned.
Prototype:
inline float fmax(float x, float y);
Remarks:
This function returns x if it is greater than y; otherwise it returns y.
Parameters:
float x
One of the floating point values used in the comparison.
float y
One of the floating point values used in the comparison.
Prototype:
inline float fmin(float x, float y);
Remarks:
This function returns x if it is less than y; otherwise it returns y.
Parameters:
float x
One of the floating point values used in the comparison.
float y
One of the floating point values used in the comparison.
Prototype:
inline AColor AComp(AColor cbot, AColor ctop);
Remarks:
This function performs an alpha-composite of ctop on top of cbot, assuming pre-multiplied alpha.
This is defined as:
{
float ia = 1.0f - ctop.a;
return (ctop + ia*cbot);
}
Parameters:
AColor cbot
The color that is composited over.
AColor ctop
The color to composite on top.
Return Value:
The composited color.
Prototype:
void CellFunction(Point3 v,int n,float *dist,int *celIDs=NULL,Point3 *grads=NULL,float gradSmooth=0.0f);
Remarks:
This is the noise function used by the 3ds max Cellular texture. The idea is that there is a set of cells randomly distributed through space. This function returns the distances to the closest cells.
Developers using this function should refer to the following paper upon which this function is based. A Cellular Basis Function by Steven Worley in the SIGGRAPH 1996 Conference Procedings.
Parameters:
Point3 v
The 3D input point.
int n
The number of elements in the arrays below.
float *dist
A set of distances are returned here. This is the distance to the closest cell, the second closest cell, etc.
int *celIDs=NULL
An optional array of integers to store cell IDs. This returns a value used to identify the cell. Since the functions works with a set of cells distributed through space, if two input points returned the same closest cell, then they would both have this same cell ID for their closest cell.
This is used in the Cellular texture to modulate the color. The cell color is varied by some random amount by using this value is used as the random seed. Thus the value is constant throughout the cell. See the function RandFromCellID(int id) below.
Point3 *grads=NULL
An optional array point Point3s used to get the partial derivatives with respect to X, Y and Z for the function. This is used for bump mapping.
float gradSmooth=0.0f
This equate to the 'Bump Smoothing' spinner in the Cellular texmap UI. The derivative of the function (the distance to the closest cell) has a discontinuity as it switches from cell to cell. Thus the gradients above have a discontinuity. This value basically smoothes off the discontinuity. The range is 0.0 to 1.0.
Prototype:
void FractalCellFunction(Point3 v,float iterations, float lacunarity,int n,float *dist,int *celIDs=NULL,Point3 *grads=NULL,float gradSmooth=0.0f);
Remarks:
This is a fractal version of above. It has additional parameter for iterations and lacunariy.
Parameters:
Point3 v
The 3D input point.
float iterations
This corresponds to the 'Interations' parameter in the Celluar UI. Varying this value gives different results.
float lacunarity
The is the 'Roughness' parameter in the Cellular UI. Varying this value gives different results.
int n
The number of elements in the arrays below.
float *dist
A set of distances are returned here. This is the distance to the closest cell, the second closest cell, etc.
int *celIDs=NULL
An optional array of integers to store cell IDs. This returns a value used to identify the cell. Since the functions works with a set of cells distributed through space, if two input points returned the same closest cell, then they would both have this same cell ID for their closest cell.
This is used in the Cellular texture to modulate the color. The cell color is varied by some random amount by using this value is used as the random seed. Thus the value is constant throughout the cell. See the function RandFromCellID(int id) below.
Point3 *grads=NULL
An optional array point Point3s used to get the partial derivatives with respect to X, Y and Z for the function. This is used for bump mapping.
float gradSmooth=0.0f
This equate to the 'Bump Smoothing' spinner in the Cellular texmap UI. The derivative of the function (the distance to the closest cell) has a discontinuity as it switches from cell to cell. Thus the gradients above have a discontinuity. This value basically smoothes off the discontinuity. The range is 0.0 to 1.0.
Prototype:
float RandFromCellID(int id);
Remarks:
Returns a random number in the range 0.0 to 1.0 based on the cellID passed.
Parameters:
int id
The seed for the random number generator.
Prototype:
void setdebug(int i);
Remarks:
This function is used internally.