Rotation Concepts
See Also: Class Quat, Class AngAxis, Class Matrix3.
Overview
This section describes the different ways rotation is represented in the 3ds max SDK and the various classes used in storing and interpolating rotation.
There are several class used in 3ds max that describe rotations in 3D space. These classes are Quat, AngAxis, and Matrix3. There are also methods that convert between these classes.
The Visualization of Rotation Space
The set of all rotations in space may be visualized as:
1) The set of all unit length axis vectors with one endpoint centered at the sphere center (0,0,0) and the other endpoint on the surface of the unit sphere.
2) The set of rotations about each vector axis (rotations about the radius vectors that point to each endpoint on the sphere).
One way to visualize this is to imagine that you could nail a dinner plate to the surface of a ball that is fixed in space (with the top surface of the plate facing the center of the ball, and the nail going from the center of the plate to the center of the sphere -- see the figure below). For each nailed position on the ball, imagine you can rotate the plate about the nail (axis). The point of placement of the nail on the ball, and the plate's rotation about it describes each of the possible rotations of the plate in a unique way.
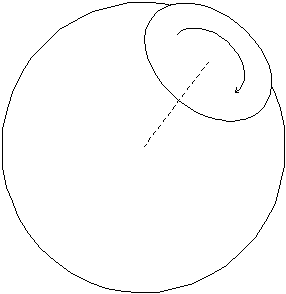
Unit sphere with axis and plate shown.
Quaternion Representation of Rotation
A quaternion may be visualized in a similar way:
1) An arbitrary unit length axis vector (one of the endpoints on the unit sphere...or the nail position).
2) A rotation about the axis (one on the rotations about the radius vectors that point to each endpoint on the sphere).
In the simplest terms, the rotational space described by each quaternion is a 3D unit vector plus a rotation. The Quat class has four public data members that store this information:
float x, y, z, w;
A normalized quaternion can represent -PI to +PI rotation -- that is -180 to 180 degrees of rotation. Quaternions use the left-hand rule for determining positive rotation.
AngAxis Representation of Rotation
This class is similar to a quaternion, except that a normalized quaternion only represents -PI to +PI rotation (that is -180 to 180 degrees of rotation). The AngAxis class can instead have any number of revolutions stored. It has two public data members:
Point3 axis;
float angle;
The axis is similar to the values in the Quat class. The angle value can represent any rotation amount in radians.
Matrix Representation of Rotation
A matrix may be used to describe rotation. See the Advanced Topics section on Matrix Representations of 3D Transformations for more information. That section describes not only rotation, but translation and scaling as represented by matrices.
Euler Angles
Multiple rotations are not independent. When you rotate something twice, the second rotation rotates the first rotation. For this reason, the order of rotation is important. The 3ds max Euler angle controller, by default, has an XYZ ordering. That is, the first rotation is done along the X axis, then along the Y axis, and finally along the Z axis. In other words, the default Euler angle controller has a type of EULERTYPE_XYZ (described below). The 3ds max local Euler angle controller is similar, but specifies rotations around an object's local coordinates instead of the world coordinates. It has a type of (EULERTYPE_XYZ | EULERTYPE_RF).
The SDK provides functions for converting from a Matrix3 to Euler angles using various rotation orderings. You need the different types because you get different interpolation of the float values with the each type.
Prototype:
void MatrixToEuler(const Matrix3 &mat, float *ang, int type);
Remarks:
This function is available in release 2.0 and later only.
Converts the specified matrix to Euler angles using the type parameter to determine the order.
Parameters:
const Matrix3 &mat
The rotation matrix to convert to Euler angles.
float *ang
The result is stored here. The array ordering is based on the type parameter below.
int type
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Note: Internally, 3ds max uses static coordinate frames. OR in the EULERTYPE_RF bit if you have a special need to use a rotating coordinate frame. This is described in Ken Shoemake's paper in Graphic Gems IV, pp. 222-229.
Prototype:
void EulerToMatrix(float *ang, Matrix3 &mat, int type);
Remarks:
This function is available in release 2.0 and later only.
Converts from the specified Euler angle format (specifying rotation with a triple of angles) to a Matrix3 format.
Parameters:
float *ang
The Euler angles to convert. The expected format is based on the type parameter below.
Matrix3 &mat
The matrix result is stored here.
int type
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Note: Internally, 3ds max uses static coordinate frames. OR in the EULERTYPE_RF bit if you have a special need to use a rotating coordinate frame. This is described in Ken Shoemake's paper in Graphic Gems IV, pp. 222-229.
Function:
void QuatToEuler(Quat &q, float *ang, int type, BOOL b=FALSE);
Remarks:
Converts the quaternion to Euler angles. When converting a quaternion to Euler angles using this method, the correct order of application of the resulting three rotations is specified by the type parameter.
Parameters:
Quat &q
The quaternion to convert.
float *ang
The angles are returned here in the same order as specified by type (for example EULERTYPE_XYZ would be ang[0]=x, ang[1]=y, ang[2]=z.)
int type
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Note: Internally, 3ds max uses static coordinate frames. OR in the EULERTYPE_RF bit if you have a special need to use a rotating coordinate frame. This is described in Ken Shoemake's paper in Graphic Gems IV, pp. 222-229.
BOOL b=FALSE
This parameter is available in release 4.0 and later only.
When this argument is set to false (or omitted), each function performs as it did before version 4.0. When the boolean is TRUE, the matrix is made with its terms transposed. When this transposition is specified, EulerToQuat() and QuatToEuler() are consistent with one another. (In Shiva, they have opposite handedness).
Function:
void EulerToQuat(float *ang, Quat &q, int type);
Remarks:
Converts Euler angles to a quaternion.
Parameters:
Quat &q
The quaternion result is returned here.
float *ang
The angles are specified in the same order as specified in the application (for example EULERTYPE_XYZ would be ang[0]=x, ang[1]=y, ang[2]=z.)
int type
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Note: Internally, 3ds max uses static coordinate frames. OR in the EULERTYPE_RF bit if you have a special need to use a rotating coordinate frame. This is described in Ken Shoemake's paper in Graphic Gems IV, pp. 222-229.
Handling Sign Flips when Converting a Rotation Controller to an Euler Controller
When converting any rotation controller to an Euler controller it is possible for sign flips to occur in the resulting animation. This is due to the fact that one single rotation matrix can be expressed through many different triplets of Euler angles. Sometimes the produced Euler angles are not interpolatable. There is code in the SDK which solves this problem. It samples the whole animation range and produces Euler angles that result in the same animation as the original, if interpolated. This code is generally valuable for developers who want to convert keys of any type of 3ds max controller that uses quaternions internally into a Euler angle keys (for example an export plug-in).
The code can be found in \MAXSDK\SAMPLES\CONTROLLERS\EULRCTRL.CPP in the method void EulerRotation::Copy(Control *from). The algorithm works as follows:
The code samples the entire animation range and incrementally adds up the angles for each time step. During resampling it detects possible sign flips by comparing the Euler/Quat ratio of two successive time steps. The Euler/Quat ratio is the relation of the angle difference in Euler space to the angle difference in Quat space. If this ratio is bigger than PI the rotation between the two time steps contains a flip. The Euler/Quat ratio can be determined using the SDK functions GetEulerQuatAngleRatio() or GetEulerMatAngleRatio() (see below). If a flip is detected the algorithm calculates the actual angle not containing a flip and adds it to the incremental angle.
The actual detection of the flip is dependent on the amount of rotation in between the time steps. It is obvious, that the smaller the time step, the more accurate the detection is. In the code described above a time step of 1 tick is used, which is most accurate, but also most time intensive. The THRESHHOLD value describes the maximum intented rotation allowed between two time increments. In the code described above the THRESHHOLD is 1.0 which is equal to 57 degrees of rotation (a lot of rotation for one tick).
Function:
float GetEulerQuatAngleRatio(Quat &quat1,Quat &quat2, float *euler1, float *euler2, int type = EULERTYPE_XYZ);
Remarks:
This global function is available in release 3.0 and later only.
The Euler/Quat ratio is the relation of the angle difference in Euler space to the angle difference in Quat space. If this ratio is bigger than PI the rotation between the two time steps contains a flip. See the description above for details.
Parameters:
Quat &quat1
The 'previous' rotation.
Quat &quat2
The 'current' rotation.
float *euler1
The 'previous' rotation as an euler angle.
float *euler2
The 'current' rotation as an euler angle.
int type = EULERTYPE_XYZ
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Return Value:
The Euler/Quat ratio between the time steps.
Function:
float GetEulerMatAngleRatio(Matrix3 &mat1,Matrix3 &mat2, float *euler1, float *euler2, int type = EULERTYPE_XYZ);
Remarks:
This global function is available in release 3.0 and later only.
The Euler/Matrix Angle ratio is the relation of the angle difference in Euler space to the angle difference in Matrix space. If this ratio is bigger than PI the rotation between the two time steps contains a flip. See the description above for details.
Parameters:
Matrix3 &mat1
The 'previous' rotation.
Matrix3 &mat2
The 'current' rotation.
float *euler1
The 'previous' rotation as an euler angle.
float *euler2
The 'current' rotation as an euler angle.
int type = EULERTYPE_XYZ
This parameter specifies the order of application of the angles. One of the following values:
EULERTYPE_XYZ
EULERTYPE_XZZ
EULERTYPE_YZX
EULERTYPE_YXZ
EULERTYPE_ZXY
EULERTYPE_ZYX
EULERTYPE_XYX
EULERTYPE_YZY
EULERTYPE_ZXZ
Return Value:
The Euler/Matrix Angle ratio between the time steps.