Matrix Representations of 3D Transformations

3DS Max Plug-In SDK

Overview

This section discusses the way transformation matrices are constructed and used in MAX, and various APIs that are available for working with these matrices.

Transformation matrices can be used, for example, to transfer the coordinates of an object from local space to world space, or to position nodes in the scene. The transformations these matrices provide are translation, scaling and rotation. Methods of the Matrix3 class (and several global functions) are provided to easily create transformation matrices and perform matrix arithmetic.

Matrix Fundamentals

A matrix is a two-dimensional array of numbers. In MAX, 4x3 matrices are used. For 3ds max matrices, the first number is the number of rows (4) and the second number is the number of columns (3). Thus there are a total of 12 elements.

An instance of Matrix3 has a private data member that contains the values:

float m[4][3];

The layout of these elements is shown in the following diagram:

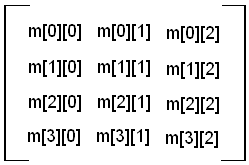
$image\matrix32_wmf.gif$

The following matrix is called the 'Identity Matrix'. This special matrix, when multiplied by a vector or another matrix, yields the original matrix.

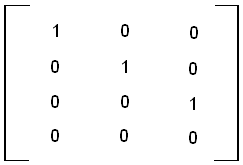
$image\matrixi_wmf.gif$

The 3ds max API provides several ways to create identity matrices. If a value of 1 is passed to the constructor of a Matrix3 it is initialized to the identity. For example

Matrix3 tmat(1); // Identity matrix

You may also use a method of Matrix3 to reset a matrix to the identity, for example:

tmat.IdentityMatrix(); // Reset to the identity matrix

You can verify if a matrix is equal to the identity by using:

BOOL isIdent = tmat.IsIdentity();

The following sections discuss the ways matrices can be used in transformations.

Multiplying a Vector by a Matrix

One thing that can be done is to multiply a vector (Point3) by a matrix (Matrix3). This results in a new vector as a result. This is often used to transform vectors from one coordinate space to another. There is a global function in the SDK that does this.

Point3 VectorTransform(const Matrix3& M, const Point3& V);

Transform the vector (Point3) with the specified matrix.

Note: In MAX, all vectors are assumed to be row vectors. Under this assumption, multiplication of a vector with a matrix using the * operator can be written either way (Matrix*Vector or Vector*Matrix), for ease of use, and the result is the same -- the (row) vector transformed by the matrix.

Multiplying Two Matrices

It is often also very useful to compute the multiplication of a matrix by another matrix. This produces a matrix as the result. Matrix multiplication is associate but not commutative. That is, AB is not the same as BA, but (AB)C is the same as A(BC). This property is very useful since separate matrix transformations can be concatenated together and then all applied at once. 3ds max provides several methods to perform matrix multiplication; each are operators of the Matrix3 class.

Matrix3& operator*=(const Matrix3& M);

Multiplies this Matrix3 by the specified Matrix3.

Matrix3 operator*(const Matrix3&) const;

Performs matrix multiplication.

Scaling

Now that we have seen some basic matrix math, let's see how we can create matrices capable of performing typical transformations. Scale transformations can be used, for example, to multiply each component of a vector by a scale factor. Scale transformations use the following matrix positions:

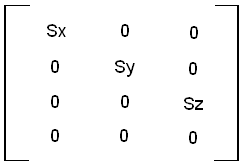
$image\matrixs_wmf.gif$

The following global function is provided in the API to create a scale matrix given a Point3 with the individual scale factors (the scale factors are in the x, y, z data members of the Point3):

Matrix3 ScaleMatrix(const Point3& s);

Builds a new matrix for use as a scale transformation.

The following method of the Matrix3 class nulls out the scale values in a matrix:

void NoScale();

This method nulls the scale portion of the matrix.

Translation

Translation matrices use the following matrix positions:

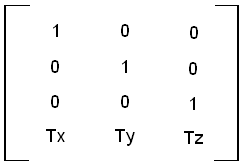
$image\matrixt_wmf.gif$

There are global functions in the 3ds max API to create these translation matrices and to apply translation to existing matrices. Several of these are given below:

Matrix3 TransMatrix(const Point3& p);

Builds a new matrix for use as a translation transformation.

A method of Matrix3 allows the translation portion of the matrix to be set.

void SetTrans(const Point3 p)

Sets the translation portion of this matrix to the specified values.

void NoTrans();

This method zeros the translation portion of this matrix.

One can also retrieve the translation portion of a matrix using the Matrix3 method:

Point3 GetTrans();

Returns the translation component of this matrix.

Rotation

The cells in a rotation matrix are the sines and cosines of the angle of rotation. In the Matrix3 right-handed coordinate system, positive angles move in a counterclockwise direction, when looking down an axis from positive to negative. In the diagram below, the cones along the XYZ axes point in the positive direction, and the cones in the circles around each axis point in the positive direction of rotation.

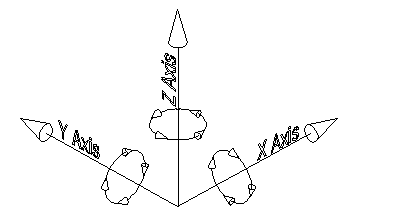
$image\axis1_wmf.gif$

The matrices for rotation about the three axes are shown below. In each case a represents the angle of rotation in radians:

X rotation

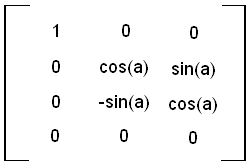
$image\matrixx_wmf.gif$

Y rotation

$image\matrixy_wmf.gif$

Z rotation

$image\matrixz_wmf.gif$

There are global functions in the 3ds max API to create these rotation matrices and to apply rotation to existing matrices. Several of these are given below:

Matrix3 RotateXMatrix(float angle);

Builds a new matrix for use as a X rotation transformation. The angle is specified in radians.

Matrix3 RotateYMatrix(float angle);

Builds a new matrix for use as a Y rotation transformation.

Matrix3 RotateZMatrix(float angle);

Builds a new matrix for use as a Z rotation transformation.

Developer can also remove the rotation from a given matrix using the Matrix3 method:

void NoRot();

This method nulls the rotation portion of the matrix.

Creating Quaternions from Rotation Matrices

A quaternion can be created from a rotation matrix. By passing the Matrix3 to the constructor of the Quat, its rotation values are used to initialize the quaternion. The following code shows an example of this. It takes a Point3 v and creates a quaternion based on the angles stored after snapping them using the current 3ds max angle snap settings.

Matrix3 mat;

mat.IdentityMatrix();

mat.RotateX(ip->SnapAngle(v.x));

mat.RotateY(ip->SnapAngle(v.y));

mat.RotateZ(ip->SnapAngle(v.z));

Quat q(mat);

A Matrix3 as an Axis System

A Matrix3 can also be used to specify an axis system. For example, the INode method Rotate() is used to rotate a node about a specified axis system. One of the arguments to this method is a Matrix3 that specifies this axis system. Essentially, a matrix is just an axis system.

For example, if you think of an axis tripod in a viewport, this is basically all the information a matrix has. The axis tripod has three vectors (the directions of the axes: X, Y, Z) and a position in space (the point where the axes converge). A transformation matrix holds this same information. The 0th row of a matrix is the X vector, the 1st row of the matrix is the Y vector, the 2nd row of the matrix is the Z vector, and the 3rd row of the matrix is the position.

You can picture this if you consider the identity matrix. Its 0th row (X) is [ 1 0 0 ] and this is just a vector along the X axis. Its 1st row (Y) is [ 0 1 0 ] and this is simply a vector along the Y axis. Its 2nd row (Z) is [ 0 0 1 ] and this is just a vector along the Z axis. And the 3rd row (position) is [ 0 0 0] and this is the origin. Therefore the identity matrix is just an axis system without any rotation, positioned at the origin. This same thing holds true for any transformation matrix, it's just not as easy to visualize as it is with the identity matrix. Therefore, any transformation matrix is really just an axis system.

To construct an axis system then, you can simply create an identity matrix, and apply transformations to the matrix to put the matrix into the coordinate system you need. For example, if you had an axis system that was rotated 45 degrees about the Z axis and centered at (10, 20, 30) you could use the following code to build it:

Matrix3 mat(1); // Identity

mat.RotateZ(DegToRad(45.0f));

mat.SetTrans(Point3(10.0f, 20.0f, 30.0f));

Transformation Matrix Demonstration Program

There is a program available in \MAXSDK\SAMPLES\HOWTO\TMATTEST\TMATTEST.CPP that shows visually how matrices are constructed for move/rotate/scale transformations. This program also shows the results of some of the INode methods that return transformation matrices (for example, GetNodeTM(), GetObjectTM(), etc.). Developers can load this project into VC++ and build it. Then copy the DLU from \MAXSDK\PLUGIN\TMATTEST.DLU into the STDPLUGS directory where 3ds max can load it. To run it select TMatTest from the HowTo section of the Utilities menu. The program operates on the first object in the selection set. Create a node in the scene (for instance a Box) and experiment with animating the node, binding it to space warps, etc., and viewing the resulting matrices returned from the INode methods. You can also build transformations from scratch and apply them to the first selected object.

previous page start next page