Calculates the least squares fit for a line represented by the following equation:

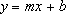
where m is the slope and b is the intercept.

Calculates the least squares fit through points by using the following equation:

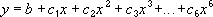
where b and 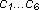are constants.

Calculates the least squares fit through points by using the following equation:

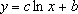
where c and b are constants, and ln is the natural logarithm function.

Calculates the least squares fit through points by using the following equation:

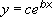
where c and b are constants, and e is the base of the natural logarithm.

Calculates the least squares fit through points by using the following equation:

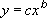
where c and b are constants.

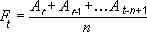
Note   The number of points in a moving average trendline equals the total number of points in the series less the number you specify for the period.

The R-squared value, also known as the coefficient of determination, is an indicator that ranges in value from 0 to 1 and reveals how closely the estimated values for the trendline correspond to your actual data. A trendline is most reliable when its R-squared value is at or near 1. When you fit a trendline to your data, the Microsoft Office Chart Component automatically calculates the R-squared value for the trendline by using the following equation:

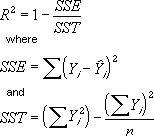
Note   The R-squared value you can display with a trendline is not an adjusted R-squared value. For logarithmic, power, and exponential trendlines, the Microsoft Office Chart Component uses a transformed regression model.