BINOM.FORDELING

Returnerer den individuelle binomiske sannsynlighetsfordelingen. Bruk BINOM.FORDELING ved løsning av problemer med et bestemt antall tester eller forsøk når utfallene av hvert forsøk bare kan være vellykket eller mislykket, når prøvene er uavhengige og når sannsynligheten for et vellykket utfall er konstant gjennom hele eksperimentet. BINOM.FORDELING kan for eksempel brukes til å beregne sannsynligheten for at to av de tre neste barna som fødes, skal være gutter.

Syntaks

BINOM.FORDELING(tall_s;forsøk;sannsynlighet_s,kumulativ)

Antall_s    er antall forsøk med vellykket utfall.

Forsøk    er antall uavhengige forsøk.

Sannsynlighet_s    er sannsynligheten for å lykkes ved hvert forsøk.

Kumulativ    er en logisk verdi som bestemmer funksjonens form. Hvis kumulativ er lik SANN, returnerer BINOM.FORDELING den kumulative fordelingsfunksjonen, eller sannsynligheten for at det maksimalt er antall_s vellykkede forsøk. Hvis kumulativ er USANN, returneres funksjonen for sannsynlig tetthet, som er sannsynligheten for at det blir nøyaktig antall_s vellykkede utfall.

Obs!

• Desimalene i antall_s og forsøk strykes, slik at tallene blir heltall.
• Hvis antall_s, forsøk eller sannsynlighet_s ikke er numeriske verdier, returnerer BINOM.FORDELING feilverdien #VERDI!.
• Hvis antall_s < 0 eller antall_s > forsøk, returnerer BINOM.FORDELING feilverdien #NUM!.
• Hvis sannsynlighet_s < 0 eller sannsynlighet_s > 1, returnerer BINOM.FORDELING feilverdien #NUM!.
• Den binomiske funksjonen for sannsynlig tetthet er:

  

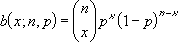
  der:

  

  er lik KOMBINASJON(n;x).

  Obs!  KOMBINASJON-funksjonen brukes her til å illustrere den matematiske formelen som brukes av funksjonen BINOM.FORDELING. Det er ikke en funksjon som kan brukes i en liste.

  Den kumulative binomiske fordelingen er:

  

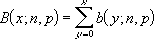
Eksempel