I/Q Data

I/Q data is an alternative method of describing the magnitude and phase data of a signal.

A sinusoidal wave can be written in polar coordinate form as shown in the following equation:

f(t) = Acos(2ft + φ)

where

A is the amplitude

2f is the frequency

φ is the phase

A sinusoidal wave can also be represented in a complex Cartesian coordinate system by its real and complex components such that the in-phase (I) component can be written as

I(t) = Acos(φ)cos(2ft)

and the quadrature (Q) component can be written as

Q(t) = Asin(φ)sin(2ft)

Graphically, I and Q projections of the polar coordinate sinusoidal wave are on the x and y axis, respectively, as illustrated in the following graph.

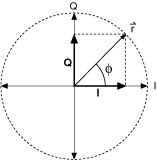
In the preceding figure, the sinusoidal wave frequency is shown as the rotational rate of the vector 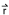around the circle.

The vector magnitude (M) is given by

M = (I(t)² + Q(t)²)^1/2

and the vector phase is given by

φ = tan^–1(Q/I).

While magnitude and phase data seem more intuitive, hardware design concerns make I and Q data the better choice for RF waveforms. I/Q representation provides an effective way to visualize and measure the quality of modulation. The following figure is a generic block diagram of an I/Q demodulator, which takes an RF signal and separates out the I and Q component from that incoming RF signal.

The following figure is a generic block diagram of an I/Q demodulator.

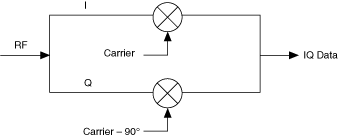
The circles with an 'X' represent mixers. The I/Q modulator is represented here as part of a downconverter module. The incoming message signal splits and one signal is multiplied by an in-phase carrier signal (I) while the other signal is multiplied by a quadrature signal (Q). This multiplication separates the in-phase and quadrature components from the incoming signal.