Returns the confidence interval for a population mean with a normal distribution. The confidence interval is a range on either side of a sample mean. For example, if you order a product through the mail, you can determine, with a particular level of confidence, the earliest and latest the product will arrive.
Syntax
CONFIDENCE(alpha,standard_dev,size)
Alpha is the significance level used to compute the confidence level. The confidence level equals 100*(1 - alpha)%, or in other words, an alpha of 0.05 indicates a 95 percent confidence level.
Standard_dev is the population standard deviation for the data range and is assumed to be known.
Size is the sample size.
Remarks
- If any argument is nonnumeric, CONFIDENCE returns the #VALUE! error value.
- If alpha ≤ 0 or alpha ≥ 1, CONFIDENCE returns the #NUM! error value.
- If standard_dev ≤ 0, CONFIDENCE returns the #NUM! error value.
- If size is not an integer, it is truncated.
- If size < 1, CONFIDENCE returns the #NUM! error value.
- If we assume alpha equals 0.05, we need to calculate the area under the standard normal curve that equals (1 - alpha), or 95 percent. This value is ± 1.96. The confidence interval is therefore:
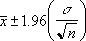
Example
Suppose we observe that, in our sample of 50 commuters, the average length of travel to work is 30 minutes with a population standard deviation of 2.5. We can be 95 percent confident that the population mean is in the interval:
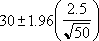
The example may be easier to understand if you copy it to a blank spreadsheet.
- Create a blank spreadsheet.
- Select the example in the Help topic.

Selecting an example from Help
- Press CTRL+C.
- In the spreadsheet, select cell A1, and press CTRL+V.
- To switch between viewing the formula that returns the result and the result in the cell, select the cell and press F2 and then ENTER, or click Commands and Options on the spreadsheet toolbar, click the Formula tab, and look in the Formula in active cell (active cell) box.
| Data | Description |
|---|---|
| 0.05 | Significance level |
| 2.5 | Standard deviation of the population |
| 50 | Sample size |
| Formula | Description (Result) |
| =CONFIDENCE(A2,A3,A4) | Confidence interval for a population mean. In other words, the average length of travel to work equals 30 ± 0.692951 minutes, or 29.3 to 30.7 minutes. (0.692951) |
 How?
How?