Open CASCADE Technology: Boolean Operations

OpenCascade

previous page next page

Open CASCADE Technology 7.2.0

Introduction
Overview
- Operators
- Parts of algorithms
Terms and Definitions
Data Structure
Root Classes
- Class BOPAlgo_Options
- Class BOPAlgo_Algo
Intersection Part
General description of the Building Part
General Fuse Algorithm
Splitter Algorithm
- Arguments
- Results
- Usage
  - API
  - DRAW
- Examples
Boolean Operations Algorithm
Section Algorithm
Volume Maker Algorithm
- Usage
- Examples
Cells Builder algorithm
- Usage
- Examples
Algorithm Limitations
- Arguments
- Intersection problems
Advanced Options
Errors and warnings reporting system
Usage
- Package BRepAlgoAPI
- Package BOPTest

Introduction

This document provides a comprehensive description of the Boolean Operation Algorithm (BOA) as it is implemented in Open CASCADE Technology. The Boolean Component contains:

General Fuse Operator (GFA),
Boolean Operator (BOA),
Section Operator (SA),
Splitter Operator (SPA).

GFA is the base algorithm for BOA, SPA, SA.

GFA has a history-based architecture designed to allow using OCAF naming functionality. The architecture of GFA is expandable, that allows creating new algorithms basing on it.

Overview

Operators

Boolean operator

The Boolean operator provides the operations (Common, Fuse, Cut) between two groups: Objects and Tools. Each group consists of an arbitrary number of arguments in terms of TopoDS_Shape.

The operator can be represented as:

R_B=B_j (G₁, G₂),

where:

R_B – result of the operation;
B_j – operation of type j (Common, Fuse, Cut);
G₁={S₁₁, S₁₂ ... S_1n1} group of arguments (Objects);
G₂={S₂₁, S₂₂ ... S_2n2} group of arguments (Tools);
n₁ – Number of arguments in Objects group;
n₂ – Number of arguments in Tools group.

Note There is an operation Cut21, which is an extension for forward Cut operation, i.e Cut21=Cut(G2, G1).

For more details see Boolean Operations Algorithm section.

General Fuse operator

The General fuse operator can be applied to an arbitrary number of arguments in terms of TopoDS_Shape.

The GFA operator can be represented as:

R_GF = GF (S₁, S₂ ... S_n),

where

R_GF – result of the operation,
S₁, S₂ ... S_n – arguments of the operation,
n – number of arguments.

The result of the Boolean operator, R_B, can be obtained from R_GF.

For example, for two arguments S₁ and S₂ the result R_GF is

R_GF = GF (S₁, S₂) = S_p1 + S_p2 + S_p12

operations_image001.svg

Operators

This Figure shows that

B_common (S₁, S₂) = S_p12;
B_cut12 (S₁, S₂) = S_p1;
B_cut21 (S₁, S₂) = S_p2;
B_fuse (S₁, S₂) = S_p1+S_p2+S_p12

R_GF=GF (S₁, S₂) = B_fuse = B_common+ B_cut12+ B_cut21.

The fact that R_GF contains the components of R_B allows considering GFA as the general case of BOA. So it is possible to implement BOA as a subclass of GFA.

For more details see General Fuse Algorithm section.

Splitter operator

The Splitter operator can be applied to an arbitrary number of arguments in terms of TopoDS_Shape. The arguments are divided into two groups: Objects and Tools. The result of SPA contains all parts that belong to the Objects but does not contain the parts that belong to the Tools.

The SPA operator can be represented as follows:

R_SPA=SPA (G₁, G₂), where:

R_SPA – is the result of the operation;
G₁={S₁₁, S₁₂ ... S_1n1} group of arguments (Objects);
G₂={S₂₁, S₂₂ ... S_2n2} group of arguments (Tools);
n₁ – Number of arguments in Objects group;
n₂ – Number of arguments in Tools group.

The result R_SPA can be obtained from R_GF .

For example, for two arguments S₁ and S₂ the result R_SPA is

R_SPA=SPA(S₁,S₂)=S_p1+S_p12.

In case when all arguments of the SPA are Objects and there are no Tools, the result of SPA is equivalent to the result of GFA.

For example, when G₁ consists of shapes S₁ and S₂ the result of SPA is

R_SPA=SPA(S₁, S₂) = S_p1 + S_p2 + S_p12 = GF (S₁, S₂)

The fact that the R_GF contains the components of R_SPA allows considering GFA as the general case of SPA. Thus, it is possible to implement SPA as a subclass of GFA.

For more details see Splitter Algorithm section.

Section operator

The Section operator SA can be applied to arbitrary number of arguments in terms of TopoDS_Shape. The result of SA contains vertices and edges in accordance with interferences between the arguments The SA operator can be represented as follows: R_SA=SA(S1, S2… Sn), where

R_SA – the operation result;
S1, S2 ... Sn – the operation arguments;
n – the number of arguments.

For more details see Section Algorithm section.

Parts of algorithms

GFA, BOA, SPA and SA have the same Data Structure (DS). The main goal of the Data Structure is to store all necessary information for input data and intermediate results.

The operators consist of two main parts:

Intersection Part (IP). The main goal of IP is to compute the interferences between sub-shapes of arguments. The IP uses DS to retrieve input data and store the results of intersections.
Building Part (BP). The main goal of BP is to build required result of an operation. This part also uses DS to retrieve data and store the results.

As it follows from the definition of operator results, the main differences between GFA, BOA, SPA and SA are in the Building Part. The Intersection Part is the same for the algorithms.

Terms and Definitions

This chapter provides the background terms and definitions that are necessary to understand how the algorithms work.

Interferences

There are two groups of interferences.

At first, each shape having a boundary representation (vertex, edge, face) has an internal value of geometrical tolerance. The shapes interfere with each other in terms of their tolerances. The shapes that have a boundary representation interfere when there is a part of 3D space where the distance between the underlying geometry of shapes is less or equal to the sum of tolerances of the shapes. Three types of shapes: vertex, edge and face – produce six types of BRep interferences:

Vertex/Vertex,
Vertex/Edge,
Vertex/Face,
Edge/Edge,
Edge/Face and
Face/Face.

At second, there are interferences that occur between a solid Z1 and a shape S2 when Z1 and S2 have no BRep interferences but S2 is completely inside of Z1. These interferences are Non-BRep interferences. There are four possible cases:

Vertex/Solid,
Edge/Solid,
Face/Solid and
Solid/Solid.

Vertex/Vertex interference

For two vertices Vi and Vj, the distance between their corresponding 3D points is less than the sum of their tolerances Tol(Vi) and Tol(Vj).

operations_image002.svg

Vertex/vertex interference

The result is a new vertex Vn with 3D point Pn and tolerance value Tol(Vn).

The coordinates of Pn and the value Tol(Vn) are computed as the center and the radius of the sphere enclosing the tolerance spheres of the source vertices (V1, V2).

Vertex/Edge interference

For a vertex Vi and an edge Ej, the distance D between 3D point of the vertex and its projection on the 3D curve of edge Ej is less or equal than sum of tolerances of vertex Tol(Vi) and edge Tol(Ej).

operations_image003.svg

Vertex/edge interference

The result is vertex Vi with the corresponding tolerance value Tol(Vi)=Max(Tol(Vi), D+Tol(Ej)), where D = distance (Pi, PPi);

and parameter t_i of the projected point PPi on 3D curve Cj of edge Ej.

Vertex/Face interference

For a vertex Vi and a face Fj the distance D between 3D point of the vertex and its projection on the surface of the face is less or equal than sum of tolerances of the vertex Tol(Vi) and the face Tol(Fj).

operations_image004.svg

Vertex/face interference

The result is vertex Vi with the corresponding tolerance value Tol(Vi)=Max(Tol(Vi), D+Tol(Fj)), where D = distance (Pi, PPi)

and parameters u_i, v_i of the projected point PPi on surface Sj of face Fj.

Edge/Edge interference

For two edges Ei and Ej (with the corresponding 3D curves Ci and Cj) there are some places where the distance between the curves is less than (or equal to) sum of tolerances of the edges.

Let us examine two cases:

In the first case two edges have one or several common parts of 3D curves in terms of tolerance.

operations_image005.svg

Edge/edge interference: common parts

The results are:

Parametric range [t_i1, t_i2 ] for 3D curve Ci of edge Ei.
Parametric range [t_j1, t_j2 ] for 3D curve Cj of edge Ej.

In the second case two edges have one or several common points in terms of tolerance.

operations_image006.svg

Edge/edge interference: common points

The result is a new vertex Vn with 3D point Pn and tolerance value Tol(Vn).

The coordinates of Pn and the value Tol(Vn) are computed as the center and the radius of the sphere enclosing the tolerance spheres of the corresponding nearest points Pi, Pj of 3D curves Ci, Cj of source edges Ei, Ej.

Parameter t_i of Pi for the 3D curve Ci.
Parameter t_j of Pj for the 3D curve Cj.

Edge/Face interference

For an edge Ei (with the corresponding 3D curve Ci) and a face Fj (with the corresponding 3D surface Sj) there are some places in 3D space, where the distance between Ci and surface Sj is less than (or equal to) the sum of tolerances of edge Ei and face Fj.

Let us examine two cases:

In the first case Edge Ei and Face Fj have one or several common parts in terms of tolerance.

operations_image007.svg

Edge/face interference: common parts

The result is a parametric range [t_i1, t_i2] for the 3D curve Ci of the edge Ei.

In the second case Edge Ei and Face Fj have one or several common points in terms of tolerance.

operations_image008.svg

Edge/face interference: common points

The result is a new vertex Vn with 3D point Pn and tolerance value Tol(Vn).

Parameter t_i of Pi for the 3D curve Ci.
Parameters u_i and v_i of the projected point PPi on the surface Sj of the face Fj.

Face/Face Interference

For a face Fi and a face Fj (with the corresponding surfaces Si and Sj) there are some places in 3D space, where the distance between the surfaces is less than (or equal to) sum of tolerances of the faces.

operations_image009.svg

Face/face interference: common curves

In the first case the result contains intersection curves C_ijk (k = 0, 1, 2…k_N, where k_N is the number of intersection curves with corresponding values of tolerances Tol(C_ijk).

operations_image010.svg

Face/face interference: common points

In the second case Face Fi and face Fj have one or several new vertices V_ijm, where m=0,1,2, ... mN, mN is the number of intersection points.

The coordinates of a 3D point P_ijm and the value Tol(V_ijm) are computed as the center and the radius of the sphere enclosing the tolerance spheres of the corresponding nearest points Pi, Pj of the surface Si, Sj of source shapes Fi, Fj.

Parameters u_j, v_j belong to point PPj projected on surface Sj of face Fj.
Parameters u_i and v_i belong to point PPi projected on surface Si of face Fi.

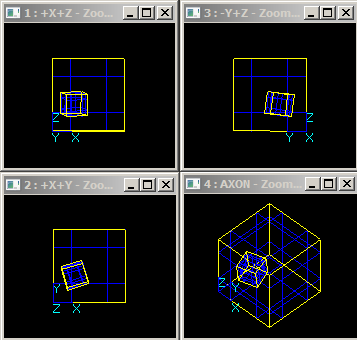
Vertex/Solid Interference

For a vertex Vi and a solid Zj there is Vertex/Solid interference if the vertex Vi has no BRep interferences with any sub-shape of Zj and Vi is completely inside the solid Zj.

Vertex/Solid Interference

Edge/Soild Interference

For an edge Ei and a solid Zj there is Edge/Solid interference if the edge Ei and its sub-shapes have no BRep interferences with any sub-shape of Zj and Ei is completely inside the solid Zj.

Edge/Solid Interference

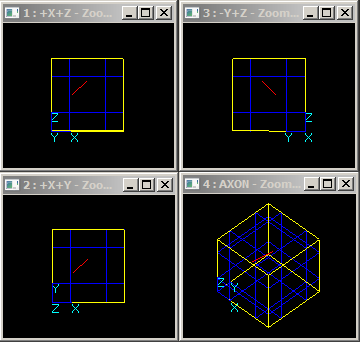
Face/Soild Interference

For a face Fi and a solid Zj there is Face/Solid interference if the face Fi and its sub-shapes have no BRep interferences with any sub-shape of Zj and Fi is completely inside the solid Zj.

Face/Solid Interference

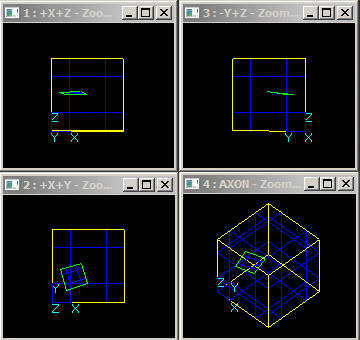
Solid/Soild Interference

For a solid Zi and a solid Zj there is Solid/Solid interference if the solid Zi and its sub-shapes have no BRep interferences with any sub-shape of Zj and Zi is completely inside the solid Zj.

Solid/Solid Interference

Computation Order

The interferences between shapes are computed on the basis of increasing of the dimension value of the shape in the following order:

Vertex/Vertex,
Vertex/Edge,
Edge/Edge,
Vertex/Face,
Edge/Face,
Face/Face,
Vertex/Solid,
Edge/Solid,
Face/Solid,
Solid/Solid.

This order allows avoiding the computation of redundant interferences between upper-level shapes Si and Sj when there are interferences between lower sub-shapes Sik and Sjm.

Results

The result of the interference is a shape that can be either interfered shape itself (or its part) or a new shape.
The result of the interference is a shape with the dimension value that is less or equal to the minimal dimension value of interfered shapes. For example, the result of Vertex/Edge interference is a vertex, but not an edge.
The result of the interference splits the source shapes on the parts each time as it can do that.

Paves

The result of interferences of the type Vertex/Edge, Edge/Edge and Edge/Face in most cases is a vertex (new or old) lying on an edge.

The result of interferences of the type Face/Face in most cases is intersection curves, which go through some vertices lying on the faces.

The position of vertex Vi on curve C can be defined by a value of parameter t_i of the 3D point of the vertex on the curve. Pave PVi on curve C is a structure containing the vertex Vi and correspondent value of the parameter t_i of the 3D point of the vertex on the curve. Curve C can be a 3D or a 2D curve.

operations_image011.svg

Paves

Two paves PV1 and PV2 on the same curve C can be compared using the parameter value

PV1 > PV2 if t1 > t2

The usage of paves allows binding of the vertex to the curve (or any structure that contains a curve: edge, intersection curve).

Pave Blocks

A set of paves PVi (i=1, 2...nPV), where nPV is the number of paves] of curve C can be sorted in the increasing order using the value of parameter t on curve C.

A pave block PBi is a part of the object (edge, intersection curve) between neighboring paves.

operations_image012.svg

Pave Blocks

Any finite source edge E has at least one pave block that contains two paves PVb and PVe:

Pave PVb corresponds to the vertex Vb with minimal parameter t_b on the curve of the edge.
Pave PVe corresponds to the vertex Ve with maximal parameter t_e on the curve of the edge.

Shrunk Range

Pave block PV of curve C is bounded by vertices V1 and V2 with tolerance values Tol(V1) and Tol(V2). Curve C has its own tolerance value Tol(C):

In case of edge, the tolerance value is the tolerance of the edge.
In case of intersection curve, the tolerance value is obtained from an intersection algorithm.

operations_image013.svg

Shrunk Range

The theoretical parametric range of the pave block is [t1C, t2C].

The positions of the vertices V1 and V2 of the pave block can be different. The positions are determined by the following conditions:

Distance (P1, P1c) is equal or less than Tol(V1) + Tol(C)

Distance (P2, P2c) is equal or less than Tol(V2) + Tol(C)

The Figure shows that each tolerance sphere of a vertex can reduce the parametric range of the pave block to a range [t1S, t2S]. The range [t1S, t2S] is the shrunk range of the pave block.

The shrunk range of the pave block is the part of 3D curve that can interfere with other shapes.

Common Blocks

The interferences of the type Edge/Edge, Edge/Face produce results as common parts.

In case of Edge/Edge interference the common parts are pave blocks that have different base edges.

operations_image014.svg

Common Blocks: Edge/Edge interference

If the pave blocks PB₁, PB₂…PB_NbPB , where NbPB is the number of pave blocks have the same bounding vertices and geometrically coincide, the pave blocks form common block CB.

In case of Edge/Face interference the common parts are pave blocks lying on a face(s).

operations_image015.svg

Common Blocks: Edge/Face interference

If the pave blocks PBi geometrically coincide with a face Fj, the pave blocks form common block CB.

In general case a common block CB contains:

Pave blocks PBi (i=0,1,2, 3… NbPB).
A set of faces Fj (j=0,1... NbF), NbF – number of faces.

FaceInfo

The structure FaceInfo contains the following information:

Pave blocks that have state In for the face;
Vertices that have state In for the face;
Pave blocks that have state On for the face;
Vertices that have state On for the face;
Pave blocks built up from intersection curves for the face;
Vertices built up from intersection points for the face.

operations_image016.svg

Face Info

In the figure, for face F1:

Pave blocks that have state In for the face: PB_in1.
Vertices that have state In for the face: V_in1.
Pave blocks that have state On for the face: PB_on11, PB_on12, PB_on2, PB_on31, PB_on32, PB_on4.
Vertices that have state On for the face: V1, V2, V3, V4, V5, V6.
Pave blocks built up from intersection curves for the face: PB_sc1.
Vertices built up from intersection points for the face: none

Data Structure

Data Structure (DS) is used to:

Store information about input data and intermediate results;
Provide the access to the information;
Provide the links between the chunks of information.

This information includes:

Arguments;
Shapes;
Interferences;
Pave Blocks;
Common Blocks.

Data Structure is implemented in the class BOPDS_DS.

Arguments

The arguments are shapes (in terms of TopoDS_Shape):

Number of arguments is unlimited.
Each argument is a valid shape (in terms of BRepCheck_Analyzer).
Each argument can be of one of the following types (see the Table):

No	Type	Index of Type
1	COMPOUND	0
2	COMPSOLID	1
3	SOLID	2
4	SHELL	3
5	FACE	4
6	WIRE	5
7	EDGE	6
8	VERTEX	7

The argument of type 0 (COMPOUND) can include any number of shapes of an arbitrary type (0, 1…7).
The argument should not be self-interfered, i.e. all sub-shapes of the argument that have geometrical coincidence through any topological entities (vertices, edges, faces) must share these entities.
There are no restrictions on the type of underlying geometry of the shapes. The faces or edges of arguments S_i can have underlying geometry of any type supported by Open CASCADE Technology modeling algorithms (in terms of GeomAbs_CurveType and GeomAbs_SurfaceType).
The faces or edges of the arguments should have underlying geometry with continuity that is not less than C1.

Shapes

The information about Shapes is stored in structure BOPDS_ShapeInfo. The objects of type BOPDS_ShapeInfo are stored in the container of array type. The array allows getting the access to the information by an index (DS index). The structure BOPDS_ShapeInfo has the following contents:

Name	Contents
myShape	Shape itself
myType	Type of shape
myBox	3D bounding box of the shape
mySubShapes	List of DS indices of sub-shapes
myReference	Storage for some auxiliary information
myFlag	Storage for some auxiliary information

Interferences

The information about interferences is stored in the instances of classes that are inherited from class BOPDS_Interf.

Name	Contents
BOPDS_Interf	Root class for interference
Index1	DS index of the shape 1
Index2	DS index of the shape 2
BOPDS_InterfVV	Storage for Vertex/Vertex interference
BOPDS_InterfVE	Storage for Vertex/Edge interference
myParam	The value of parameter of the point of the vertex on the curve of the edge
BOPDS_InterfVF	Storage for Vertex/Face interference
myU, myV	The value of parameters of the point of the vertex on the surface of the face
BOPDS_InterfEE	Storage for Edge/Edge interference
myCommonPart	Common part (in terms of IntTools_CommonPart )
BOPDS_InterfEF	Storage for Edge/Face interference
myCommonPart	Common part (in terms of IntTools_CommonPart )
BOPDS_InterfFF	Storage for Face/Face interference
myTolR3D, myTolR2D	The value of tolerances of curves (points) reached in 3D and 2D
myCurves	Intersection Curves (in terms of BOPDS_Curve)
myPoints	Intersection Points (in terms of BOPDS_Point)
BOPDS_InterfVZ	Storage for Vertex/Solid interference
BOPDS_InterfEZ	Storage for Edge/Solid interference
BOPDS_InterfFZ	Storage for Face/Solid interference
BOPDS_InterfZZ	Storage for Solid/Solid interference

The Figure shows inheritance diagram for BOPDS_Interf classes.

operations_image017.svg

BOPDS_Interf classes

Pave, PaveBlock and CommonBlock

The information about the pave is stored in objects of type BOPDS_Pave.

Name	Contents
BOPDS_Pave
myIndex	DS index of the vertex
myParam	Value of the parameter of the 3D point of vertex on curve.

The information about pave blocks is stored in objects of type BOPDS_PaveBlock.

Name	Contents
BOPDS_PaveBlock
myEdge	DS index of the edge produced from the pave block
myOriginalEdge	DS index of the source edge
myPave1	Pave 1 (in terms of BOPDS_Pave)
myPave2	Pave 2 (in terms of BOPDS_Pave)
myExtPaves	The list of paves (in terms of BOPDS_Pave) that is used to store paves lying inside the pave block during intersection process
myCommonBlock	The reference to common block (in terms of BOPDS_CommonBlock) if the pave block is a common block
myShrunkData	The shrunk range of the pave block

To be bound to an edge (or intersection curve) the structures of type BOPDS_PaveBlock are stored in one container of list type (BOPDS_ListOfPaveBlock).
In case of edge, all the lists of pave blocks above are stored in one container of array type. The array allows getting the access to the information by index of the list of pave blocks for the edge. This index (if exists) is stored in the field myReference.

The information about common block is stored in objects of type BOPDS_CommonBlock.

Name	Contents
BOPDS_CommonBlock
myPaveBlocks	The list of pave blocks that are common in terms of Common Blocks
myFaces	The list of DS indices of the faces, on which the pave blocks lie.

Points and Curves

The information about intersection point is stored in objects of type BOPDS_Point.

Name	Contents
BOPDS_Point
myPnt	3D point
myPnt2D1	2D point on the face1
myPnt2D2	2D point on the face2

The information about intersection curve is stored in objects of type BOPDS_Curve.

Name	Contents
BOPDS_Curve
myCurve	The intersection curve (in terms of IntTools_Curve )
myPaveBlocks	The list of pave blocks that belong to the curve
myBox	The bounding box of the curve (in terms of Bnd_Box )

FaceInfo

The information about FaceInfo is stored in a structure BOPDS_FaceInfo. The structure BOPDS_FaceInfo has the following contents.

Name	Contents
BOPDS_FaceInfo
myPaveBlocksIn	Pave blocks that have state In for the face
myVerticesIn	Vertices that have state In for the face
myPaveBlocksOn	Pave blocks that have state On for the face
myVerticesOn	Vertices that have state On for the face
myPaveBlocksSc	Pave blocks built up from intersection curves for the face
myVerticesSc	Vertices built up from intersection points for the face +

The objects of type BOPDS_FaceInfo are stored in one container of array type. The array allows getting the access to the information by index. This index (if exists) is stored in the field myReference.

Root Classes

Class BOPAlgo_Options

The class BOPAlgo_Options provides the following options for the algorithms:

Set the appropriate memory allocator;
Check the presence of the Errors and Warnings;
Turn on/off the parallel processing;
Set the additional tolerance for the operation;
Break the operations by user request.

Class BOPAlgo_Algo

The class BOPAlgo_Algo provides the base interface for all algorithms:

Perform the operation;
Check the input data;
Check the result.

Intersection Part

Intersection Part (IP) is used to

Initialize the Data Structure;
Compute interferences between the arguments (or their sub-shapes);
Compute same domain vertices, edges;
Build split edges;
Build section edges;
Build p-curves;
Store all obtained information in DS.

IP is implemented in the class BOPAlgo_PaveFiller.

Diagram for Class BOPAlgo_PaveFiller

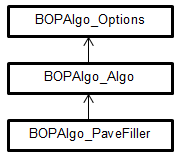
The description provided in the next paragraphs is coherent with the implementation of the method BOPAlgo_PaveFiller::Perform().

Initialization

The input data for the step is the Arguments. The description of initialization step is shown in the Table.

No	Contents	Implementation
1	Initialization the array of shapes (in terms of Shapes). Filling the array of shapes.	BOPDS_DS::Init()
2	Initialization the array pave blocks (in terms of Pave, PaveBlock, CommonBlock)	BOPDS_DS::Init()
3	Initialization of intersection Iterator. The intersection Iterator is the object that computes intersections between sub-shapes of the arguments in terms of bounding boxes. The intersection Iterator provides approximate number of the interferences for given type (in terms of Interferences)	BOPDS_Iterator
4	Initialization of intersection Context. The intersection Context is an object that contains geometrical and topological toolkit (classifiers, projectors, etc). The intersection Context is used to cache the tools to increase the algorithm performance.	IntTools_Context

Compute Vertex/Vertex Interferences

The input data for this step is the DS after the Initialization. The description of this step is shown in the table :

No	Contents	Implementation
1	Initialize array of Vertex/Vertex interferences.	BOPAlgo_PaveFiller::PerformVV()
2	Access to the pairs of interfered shapes (nVi, nVj)k, k=0, 1…nk, where nVi and nVj are DS indices of vertices Vi and Vj and nk is the number of pairs.	BOPDS_Iterator
3	Compute the connexity chains of interfered vertices nV1C, nV2C… nVnC)k, C=0, 1…nCs, where nCs is the number of the connexity chains	BOPAlgo_Tools::MakeBlocksCnx()
4	Build new vertices from the chains VNc. C=0, 1…nCs.	BOPAlgo_PaveFiller::PerformVV()
5	Append new vertices in DS.	BOPDS_DS::Append()
6	Append same domain vertices in DS.	BOPDS_DS::AddShapeSD()
7	Append Vertex/Vertex interferences in DS.	BOPDS_DS::AddInterf()

The pairs of interfered vertices are: (nV11, nV12), (nV11, nV13), (nV12, nV13), (nV13, nV15), (nV13, nV14), (nV14, nV15), (nV21, nV22), (nV21, nV23), (nV22, nV23);
These pairs produce two chains: (nV11, nV12, nV13, nV14, nV15) and (nV21, nV22, nV23);
Each chain is used to create a new vertex, VN1 and VN2, correspondingly.

The example of connexity chains of interfered vertices is given in the image:

operations_image018.svg

Connexity chains of interfered vertices

Compute Vertex/Edge Interferences

The input data for this step is the DS after computing Vertex/Vertex interferences.

No	Contents	Implementation
1	Initialize array of Vertex/Edge interferences	BOPAlgo_PaveFiller::PerformVE()
2	Access to the pairs of interfered shapes (nVi, nEj)k k=0, 1…nk, where nVi is DS index of vertex Vi, nEj is DS index of edge Ej and nk is the number of pairs.	BOPDS_Iterator
3	Compute paves. See Vertex/Edge Interference	BOPInt_Context::ComputeVE()
4	Initialize pave blocks for the edges Ej involved in the interference	BOPDS_DS:: ChangePaveBlocks()
5	Append the paves into the pave blocks in terms of Pave, PaveBlock and CommonBlock	BOPDS_PaveBlock:: AppendExtPave()
6	Append Vertex/Edge interferences in DS	BOPDS_DS::AddInterf()

Update Pave Blocks

The input data for this step is the DS after computing Vertex/Edge Interferences.

No	Contents	Implementation
1	Each pave block PB containing internal paves is split by internal paves into new pave blocks PBN1, PBN2… PBNn. PB is replaced by new pave blocks PBN1, PBN2… PBNn in the DS.	BOPDS_DS:: UpdatePaveBlocks()

Compute Edge/Edge Interferences

The input data for this step is the DS after updating Pave Blocks.

No	Contents	Implementation
1	Initialize array of Edge/Edge interferences	BOPAlgo_PaveFiller::PerformEE()
2	Access to the pairs of interfered shapes (nEi, nEj)k, k=0, 1…nk, where nEi is DS index of the edge Ei, nEj is DS index of the edge Ej and nk is the number of pairs.	BOPDS_Iterator
3	Initialize pave blocks for the edges involved in the interference, if it is necessary.	BOPDS_DS:: ChangePaveBlocks()
4	Access to the pave blocks of interfered shapes: (PBi1, PBi2…PBiNi) for edge Ei and (PBj1, PBj2…PBjNj) for edge Ej	BOPAlgo_PaveFiller::PerformEE()
5	Compute shrunk data for pave blocks in terms of Pave, PaveBlock and CommonBlock, if it is necessary.	BOPAlgo_PaveFiller::FillShrunkData()
6	Compute Edge/Edge interference for pave blocks PBix and PBiy. The result of the computation is a set of objects of type IntTools_CommonPart	IntTools_EdgeEdge
7.1	For each CommonPart of type VERTEX: Create new vertices VNi (i =1, 2…,NbVN), where NbVN is the number of new vertices. Intersect the vertices VNi using the steps Initialization and compute Vertex/Vertex interferences as follows: a) create a new object PFn of type BOPAlgo_PaveFiller with its own DS; b) use new vertices VNi (i=1, 2…,NbVN), NbVN as arguments (in terms of TopoDs_Shape) of PFn; c) invoke method Perform() for PFn. The resulting vertices VNXi (i=1, 2…,NbVNX), where NbVNX is the number of vertices, are obtained via mapping between VNi and the results of PVn.	BOPTools_Tools::MakeNewVertex()
7.2	For each CommonPart of type EDGE: Compute the coinciding connexity chains of pave blocks (PB1C, PB2C… PNnC)k, C=0, 1…nCs, where nCs is the number of the connexity chains. Create common blocks (CBc. C=0, 1…nCs) from the chains. Attach the common blocks to the pave blocks.	BOPAlgo_Tools::PerformCommonBlocks()
8	Post-processing. Append the paves of VNXi into the corresponding pave blocks in terms of Pave, PaveBlock and CommonBlock	BOPDS_PaveBlock:: AppendExtPave()
9	Split common blocks CBc by the paves.	BOPDS_DS:: UpdateCommonBlock()
10	Append Edge/Edge interferences in the DS.	BOPDS_DS::AddInterf()

The example of coinciding chains of pave blocks is given in the image:

Coinciding chains of pave blocks

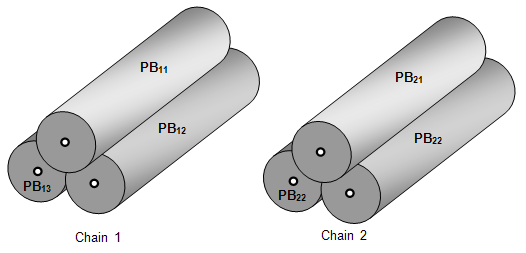
The pairs of coincided pave blocks are: (PB11, PB12), (PB11, PB13), (PB12, PB13), (PB21, PB22), (PB21, PB23), (PB22, PB23).
The pairs produce two chains: (PB11, PB12, PB13) and (PB21, PB22, PB23).

Compute Vertex/Face Interferences

The input data for this step is the DS after computing Edge/Edge interferences.

No	Contents	Implementation
1	Initialize array of Vertex/Face interferences	BOPAlgo_PaveFiller::PerformVF()
2	Access to the pairs of interfered shapes (nVi, nFj)k, k=0, 1…nk, where nVi is DS index of the vertex Vi, nFj is DS index of the edge Fj and nk is the number of pairs.	BOPDS_Iterator
3	Compute interference See Vertex/Face Interference	BOPInt_Context::ComputeVF()
4	Append Vertex/Face interferences in the DS	BOPDS_DS::AddInterf()
5	Repeat steps 2-4 for each new vertex VNXi (i=1, 2…,NbVNX), where NbVNX is the number of vertices.	BOPAlgo_PaveFiller::TreatVerticesEE()

Compute Edge/Face Interferences

The input data for this step is the DS after computing Vertex/Face Interferences.

No	Contents	Implementation
1	Initialize array of Edge/Face interferences	BOPAlgo_PaveFiller::PerformEF()
2	Access to the pairs of interfered shapes (nEi, nFj)k, k=0, 1…nk, where nEi is DS index of edge Ei, nFj is DS index of face Fj and nk is the number of pairs.	BOPDS_Iterator
3	Initialize pave blocks for the edges involved in the interference, if it is necessary.	BOPDS_DS::ChangePaveBlocks()
4	Access to the pave blocks of interfered edge (PBi1, PBi2…PBiNi) for edge Ei	BOPAlgo_PaveFiller::PerformEF()
5	Compute shrunk data for pave blocks (in terms of Pave, PaveBlock and CommonBlock) if it is necessary.	BOPAlgo_PaveFiller::FillShrunkData()
6	Compute Edge/Face interference for pave block PBix, and face nFj. The result of the computation is a set of objects of type IntTools_CommonPart	IntTools_EdgeFace
7.1	For each CommonPart of type VERTEX: Create new vertices VNi (i=1, 2…,NbVN), where NbVN is the number of new vertices. Merge vertices VNi as follows: a) create new object PFn of type BOPAlgo_PaveFiller with its own DS; b) use new vertices VNi (i=1, 2…,NbVN), NbVN as arguments (in terms of TopoDs_Shape) of PFn; c) invoke method Perform() for PFn. The resulting vertices VNXi (i=1, 2…,NbVNX), where NbVNX is the number of vertices, are obtained via mapping between VNi and the results of PVn.	BOPTools_Tools::MakeNewVertex() and BOPAlgo_PaveFiller::PerformVertices1()
7.2	For each CommonPart of type EDGE: Create common blocks (CBc. C=0, 1…nCs) from pave blocks that lie on the faces. Attach the common blocks to the pave blocks.	BOPAlgo_Tools::PerformCommonBlocks()
8	Post-processing. Append the paves of VNXi into the corresponding pave blocks in terms of Pave, PaveBlock and CommonBlock.	BOPDS_PaveBlock:: AppendExtPave()
9	Split pave blocks and common blocks CBc by the paves.	BOPAlgo_PaveFiller::PerformVertices1(), BOPDS_DS:: UpdatePaveBlock() and BOPDS_DS:: UpdateCommonBlock()
10	Append Edge/Face interferences in the DS	BOPDS_DS::AddInterf()
11	Update FaceInfo for all faces having EF common parts.	BOPDS_DS:: UpdateFaceInfoIn()

Build Split Edges

The input data for this step is the DS after computing Edge/Face Interferences.

For each pave block PB take the following steps:

No	Contents	Implementation
1	Get the real pave block PBR, which is equal to PB if PB is not a common block and to PB₁ if PB is a common block. PB₁ is the first pave block in the pave blocks list of the common block. See Pave, PaveBlock and CommonBlock.	BOPAlgo_PaveFiller::MakeSplitEdges()
2	Build the split edge Esp using the information from DS and PBR.	BOPTools_Tools::MakeSplitEdge()
3	Compute BOPDS_ShapeInfo contents for Esp	BOPAlgo_PaveFiller::MakeSplitEdges()
4	Append BOPDS_ShapeInfo contents to the DS	BOPDS_DS::Append()

Compute Face/Face Interferences

The input data for this step is DS after building Split Edges.

No	Contents	Implementation
1	Initialize array of Face/Face interferences	BOPAlgo_PaveFiller::PerformFF()
2	Access to the pairs of interfered shapes (nFi, nFj)k, k=0, 1…nk, where nFi is DS index of edge Fi, nFj is DS index of face Fj and nk is the number of pairs.	BOPDS_Iterator
3	Compute Face/Face interference	IntTools_FaceFace
4	Append Face/Face interferences in the DS.	BOPDS_DS::AddInterf()

Build Section Edges

The input data for this step is the DS after computing Face/Face interferences.

No	Contents	Implementation
1	For each Face/Face interference nFi, nFj, retrieve FaceInfo. Create draft vertices from intersection points VPk (k=1, 2…, NbVP), where NbVP is the number of new vertices, and the draft vertex VPk is created from an intersection point if VPk ≠ Vm (m = 0, 1, 2… NbVm), where Vm is an existing vertex for the faces nFi and nF,j (On or In in terms of TopoDs_Shape), NbVm is the number of vertices existing on faces nFi and nF,j and ≠ – means non-coincidence in terms of Vertex/Vertex interference.	BOPAlgo_PaveFiller::MakeBlocks()
2	For each intersection curve Cijk
2.1	Create paves PVc for the curve using existing vertices, i.e. vertices On or In (in terms of FaceInfo) for faces nFi and nFj. Append the paves PVc	BOPAlgo_PaveFiller::PutPaveOnCurve() and BOPDS_PaveBlock::AppendExtPave()
2.2	Create technological vertices Vt, which are the bounding points of an intersection curve (with the value of tolerance Tol(Cijk)). Each vertex Vt with parameter Tt on curve Cijk forms pave PVt on curve Cijk. Append technological paves.	BOPAlgo_PaveFiller::PutBoundPaveOnCurve()
2.3	Create pave blocks PBk for the curve using paves (k=1, 2…, NbPB), where NbPB is the number of pave blocks	BOPAlgo_PaveFiller::MakeBlocks()
2.4	Build draft section edges ESk using the pave blocks (k=1, 2…, NbES), where NbES is the number of draft section edges The draft section edge is created from a pave block PBk if PBk has state In or On for both faces nFi and nF,j and PBk ≠ PBm (m=0, 1, 2… NbPBm), where PBm is an existing pave block for faces nFi and nF,j (On or In in terms of FaceInfo), NbVm is the number of existing pave blocks for faces nFi and nF,j and ≠ – means non-coincidence (in terms of Vertex/Face interference).	BOPTools_Tools::MakeEdge()
3	Intersect the draft vertices VPk (k=1, 2…, NbVP) and the draft section edges ESk (k=1, 2…, NbES). For this: a) create new object PFn of type BOPAlgo_PaveFiller with its own DS; b) use vertices VPk and edges ESk as arguments (in terms of Arguments) of PFn; c) invoke method Perform() for PFn. Resulting vertices VPXk (k=1, 2… NbVPX) and edges ESXk (k=1, 2… NbESX) are obtained via mapping between VPk, ESk and the results of PVn.	BOPAlgo_PaveFiller::PostTreatFF()
4	Update face info (sections about pave blocks and vertices)	BOPAlgo_PaveFiller::PerformFF()

Build P-Curves

The input data for this step is the DS after building section edges.

No	Contents	Implementation
1	For each Face/Face interference nFi and nFj build p-Curves on nFi and nFj for each section edge ESXk.	BOPAlgo_PaveFiller::MakePCurves()
2	For each pave block that is common for faces nFi and nFj build p-Curves on nFi and nFj.	BOPAlgo_PaveFiller::MakePCurves()

Process Degenerated Edges

The input data for this step is the DS after building P-curves.

No	Contents	Implementation
	For each degenerated edge ED having vertex VD	BOPAlgo_PaveFiller::ProcessDE()
1	Find pave blocks PBi (i=1,2… NbPB), where NbPB is the number of pave blocks, that go through vertex VD.	BOPAlgo_PaveFiller::FindPaveBlocks()
2	Compute paves for the degenerated edge ED using a 2D curve of ED and a 2D curve of PBi. Form pave blocks PBDi (i=1,2… NbPBD), where NbPBD is the number of the pave blocks for the degenerated edge ED	BOPAlgo_PaveFiller::FillPaves()
3	Build split edges ESDi (i=1,2…NbESD), where ESD is the number of split edges, using the pave blocks PBDi	BOPAlgo_PaveFiller:: MakeSplitEdge()

General description of the Building Part

Building Part (BP) is used to

Build the result of the operation
Provide history information (in terms of ::Generated(), ::Modified() and ::IsDeleted()) BP uses the DS prepared by BOPAlgo_PaveFiller described at chapter 5 as input data. BP is implemented in the following classes:
BOPAlgo_Builder – for the General Fuse operator (GFA).
BOPAlgo_BOP – for the Boolean Operation operator (BOA).
BOPAlgo_Section – for the Section operator (SA).
BOPAlgo_MakerVolume – for the Volume Maker operator.
BOPAlgo_Splitter – for the Splitter operator.
BOPAlgo_CellsBuilder – for the Cells Builder operator.

Diagram for BP classes

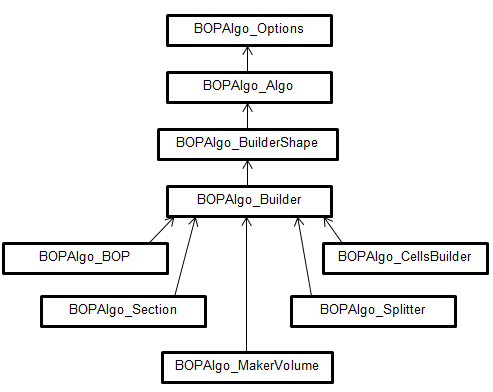
The class BOPAlgo_BuilderShape provides the interface for algorithms that have:

A Shape as the result;
History information (in terms of ::Generated(), ::Modified() and ::IsDeleted()).

General Fuse Algorithm

Arguments

The arguments of the algorithm are shapes (in terms of TopoDS_Shape). The main requirements for the arguments are described in Data Structure chapter.

Results

During the operation argument Si can be split into several parts Si1, Si2… Si1NbSp, where NbSp is the number of parts. The set (Si1, Si2… Si1NbSp) is an image of argument Si.

The result of the General Fuse operation is a compound. Each sub-shape of the compound corresponds to the certain argument shape S1, S2…Sn and has shared sub-shapes in accordance with interferences between the arguments.
For the arguments of the type EDGE, FACE, SOLID the result contains split parts of the argument.
For the arguments of the type WIRE, SHELL, COMPSOLID, COMPOUND the result contains the image of the shape of the corresponding type (i.e. WIRE, SHELL, COMPSOLID or COMPOUND). The types of resulting shapes depend on the type of the corresponding argument participating in the operation. See the table below:

No	Type of argument	Type of resulting shape	Comments
1	COMPOUND	COMPOUND	The resulting COMPOUND is built from images of sub-shapes of type COMPOUND COMPSOLID, SHELL, WIRE and VERTEX. Sets of split sub-shapes of type SOLID, FACE, EDGE.
2	COMPSOLID	COMPSOLID	The resulting COMPSOLID is built from split SOLIDs.
3	SOLID	Set of split SOLIDs
4	SHELL	SHELL	The resulting SHELL is built from split FACEs
5	FACE	Set of split FACEs
6	WIRE	WIRE	The resulting WIRE is built from split EDGEs
7	EDGE	Set of split EDGEs
8	VERTEX	VERTEX

Examples

Please, have a look at the examples, which can help to better understand the definitions.

Case 1: Three edges intersecting at a point

Let us consider three edges: E1, E2 and E3 that intersect in one 3D point.

operations_image021.svg

Three Intersecting Edges

The result of the GFA operation is a compound containing 6 new edges: E11, E12, E21, E22, E31, and E32. These edges have one shared vertex Vn1.

In this case:

The argument edge E1 has resulting split edges E11 and E12 (image of E1).
The argument edge E2 has resulting split edges E21 and E22 (image of E2).
The argument edge E3 has resulting split edges E31 and E32 (image of E3).

Case 2: Two wires and an edge

Let us consider two wires W1 (Ew11, Ew12, Ew13) and W2 (Ew21, Ew22, Ew23) and edge E1.

operations_image022.svg

Two wires and an edge

The result of the GF operation is a compound consisting of 2 wires: Wn1 (Ew11, En1, En2, En3, Ew13) and Wn2 (Ew21, En2, En3, En4, Ew23) and two edges: E11 and E12.

In this case :

The argument W1 has image Wn1.
The argument W2 has image Wn2.
The argument edge E1 has split edges E11 and E12. (image of E1). The edges En1, En2, En3, En4 and vertex Vn1 are new shapes created during the operation. Edge Ew12 has split edges En1, En2 and En3 and edge Ew22 has split edges En2, En3 and En4.

Case 3: An edge intersecting with a face

Let us consider edge E1 and face F2:

operations_image023.svg

An edge intersecting with a face

The result of the GF operation is a compound consisting of 3 shapes:

Split edge parts E11 and E12 (image of E1).
New face F21 with internal edge E12 (image of F2).

Case 4: An edge lying on a face

Let us consider edge E1 and face F2:

operations_image024.svg

An edge lying on a face

The result of the GF operation is a compound consisting of 5 shapes:

Split edge parts E11, E12 and E13 (image of E1).
Split face parts F21 and F22 (image of F2).

Case 5: An edge and a shell

Let us consider edge E1 and shell Sh2 that consists of 2 faces: F21 and F22

operations_image025.svg

An edge and a shell

The result of the GF operation is a compound consisting of 5 shapes:

Split edge parts E11, E12 , E13 and E14 (image of E1).
Image shell Sh21 (that contains split face parts F211, F212, F221 and F222).

Case 6: A wire and a shell

Let us consider wire W1 (E1, E2, E3, E4) and shell Sh2 (F21, F22).

operations_image026.svg

A wire and a shell

The result of the GF operation is a compound consisting of 2 shapes:

Image wire W11 that consists of split edge parts from wire W1: E11, E12, E13 and E14.
Image shell Sh21 that contains split face parts: F211, F212, F213, F221, F222 and F223.

Case 7: Three faces

Let us consider 3 faces: F1, F2 and F3.

Three faces

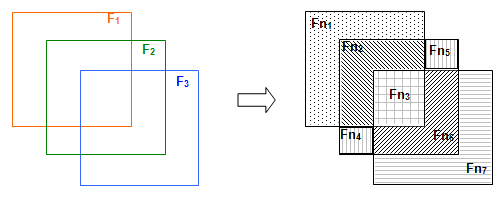
The result of the GF operation is a compound consisting of 7 shapes:

Split face parts: Fn1, Fn2, Fn3, Fn4, Fn5, Fn6 and Fn7.

Case 8: A face and a shell

Let us consider shell Sh1 (F11, F12, F13) and face F2.

A face and a shell

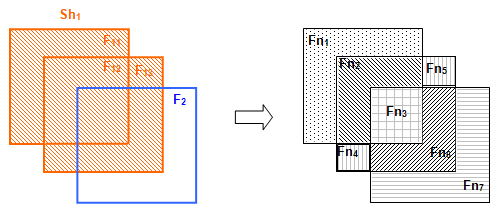
The result of the GF operation is a compound consisting of 4 shapes:

Image shell Sh11 that consists of split face parts from shell Sh1: Fn1, Fn2, Fn3, Fn4, Fn5 and Fn6.
Split parts of face F2: Fn3, Fn6 and Fn7.

Case 9: A shell and a solid

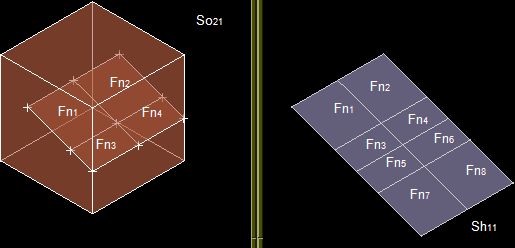
Let us consider shell Sh1 (F11, F12…F16) and solid So2.

A shell and a solid: arguments

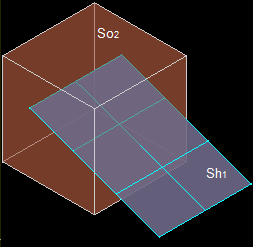
The result of the GF operation is a compound consisting of 2 shapes:

Image shell Sh11 consisting of split face parts of Sh1: Fn1, Fn2 ... Fn8.
Solid So21 with internal shell. (image of So2).

A shell and a solid: results

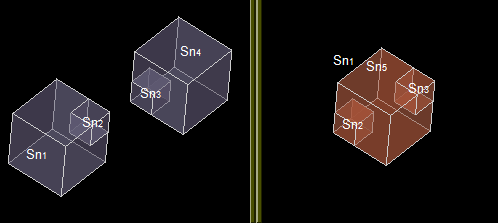
Case 10: A compound and a solid

Let us consider compound Cm1 consisting of 2 solids So11 and So12) and solid So2.

A compound and a solid: arguments

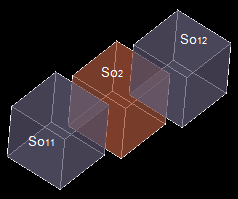
The result of the GF operation is a compound consisting of 4 shapes:

Image compound Cm11 consisting of split solid parts from So11 and So12 (Sn1, Sn2, Sn3, Sn4).
Split parts of solid So2 (Sn2, Sn3, Sn5).

A compound and a solid: results

Class BOPAlgo_Builder

GFA is implemented in the class BOPAlgo_Builder.

Fields

The main fields of the class are described in the Table:

Name	Contents
myPaveFiller	Pointer to the BOPAlgo_PaveFiller object
myDS	Pointer to the BOPDS_DS object
myContext	Pointer to the intersection Context
myImages	The Map between the source shape and its images
myShapesSD	The Map between the source shape (or split part of source shape) and the shape (or part of shape) that will be used in result due to same domain property.

Initialization

The input data for this step is a BOPAlgo_PaveFiller object (in terms of Intersection) at the state after Processing of degenerated edges with the corresponding DS.

No	Contents	Implementation
1	Check the readiness of the DS and BOPAlgo_PaveFiller.	BOPAlgo_Builder::CheckData()
2	Build an empty result of type Compound.	BOPAlgo_Builder::Prepare()

Build Images for Vertices

The input data for this step is BOPAlgo_Builder object after Initialization.

No	Contents	Implementation
1	Fill myShapesSD by SD vertices using the information from the DS.	BOPAlgo_Builder::FillImagesVertices()

Build Result of Type Vertex

The input data for this step is BOPAlgo_Builder object after building images for vertices and Type, which is the shape type (TopAbs_VERTEX).

No	Contents	Implementation
1	For the arguments of type Type. If there is an image for the argument: add the image to the result. If there is no image for the argument: add the argument to the result.	BOPAlgo_Builder::BuildResult()

Build Images for Edges

The input data for this step is BOPAlgo_Builder object after building result of type vertex.

No	Contents	Implementation
1	For all pave blocks in the DS. Fill myImages for the original edge E by split edges ESPi from pave blocks. In case of common blocks on edges, use edge ESPSDj that corresponds to the leading pave block and fill myShapesSD by the pairs ESPi/ESPSDj.	BOPAlgo_Builder::FillImagesEdges()

Build Result of Type Edge

This step is the same as Building Result of Type Vertex, but for the type Edge.

Build Images for Wires

The input data for this step is:

BOPAlgo_Builder object after building result of type Edge;
Original Shape – Wire
Type – the shape type (TopAbs_WIRE).

No	Contents	Implementation
1	For all arguments of the type Type. Create a container C of the type Type.	BOPAlgo_Builder::FillImagesContainers()
2	Add to C the images or non-split parts of the Original Shape, taking into account its orientation.	BOPAlgo_Builder::FillImagesContainers() BOPTools_Tools::IsSplitToReverse()
3	Fill myImages for the Original Shape by the information above.	BOPAlgo_Builder::FillImagesContainers()

Build Result of Type Wire

This step is the same as Building Result of Type Vertex but for the type Wire.

Build Images for Faces

The input data for this step is BOPAlgo_Builder object after building result of type Wire.

No	Contents	Implementation
1	Build Split Faces for all interfered DS shapes Fi of type FACE.
1.1	Collect all edges or their images of Fi(ESPij).	BOPAlgo_Builder::BuildSplitFaces()
1.2	Impart to ESPij the orientation to be coherent with the original one.	BOPAlgo_Builder::BuildSplitFaces()
1.3	Collect all section edges SEk for Fi.	BOPAlgo_Builder::BuildSplitFaces()
1.4	Build split faces for Fi (Fi1, Fi2…FiNbSp), where NbSp is the number of split parts (see Building faces from a set of edges for more details).	BOPAlgo_BuilderFace
1.5	Impart to (Fi1, Fi2…FiNbSp) the orientation coherent with the original face Fi.	BOPAlgo_Builder::BuildSplitFaces()
1.6	Fill the map mySplits with Fi/(Fi1, Fi2…FiNbSp)	BOPAlgo_Builder::BuildSplitFaces()
2	Fill Same Domain faces	BOPAlgo_Builder::FillSameDomainFaces
2.1	Find and collect in the contents of mySplits the pairs of same domain split faces (Fij, Fkl)m, where m is the number of pairs.	BOPAlgo_Builder::FillSameDomainFaces BOPTools_Tools::AreFacesSameDomain()
2.2	Compute the connexity chains 1) of same domain faces (F1C, F2C… FnC)k, C=0, 1…nCs, where nCs is the number of connexity chains.	BOPAlgo_Builder::FillSameDomainFaces()
2.3	Fill myShapesSD using the chains (F1C, F2C… FnC)k	BOPAlgo_Builder::FillSameDomainFaces()
2.4	Add internal vertices to split faces.	BOPAlgo_Builder::FillSameDomainFaces()
2.5	Fill myImages using myShapesSD and mySplits.	BOPAlgo_Builder::FillSameDomainFaces()

The example of chains of same domain faces is given in the image:

operations_image033.svg

Chains of same domain faces

The pairs of same domain faces are: (F11, F21), (F22, F31), (F41, F51) , (F41, F6) and (F51, F6).
The pairs produce the three chains: (F11, F21), (F22, F31) and (F41, F51, F6).

Build Result of Type Face

This step is the same as Building Result of Type Vertex but for the type Face.

Build Images for Shells

The input data for this step is:

BOPAlgo_Builder object after building result of type face;
Original Shape – a Shell;
Type – the type of the shape (TopAbs_SHELL).

The procedure is the same as for building images for wires.

Build Result of Type Shell

This step is the same as Building Result of Type Vertex but for the type Shell.

Build Images for Solids

The input data for this step is BOPAlgo_Builder object after building result of type Shell.

The following procedure is executed for all interfered DS shapes Si of type SOLID.

No	Contents	Implementation
1	Collect all images or non-split parts for all faces (FSPij) that have 3D state In Si.	BOPAlgo_Builder::FillIn3DParts ()
2	Collect all images or non-split parts for all faces of Si	BOPAlgo_Builder::BuildSplitSolids()
3	Build split solids for Si -> (Si1, Si2…SiNbSp), where NbSp is the number of split parts (see Building faces from a set of edges for more details)	BOPAlgo_BuilderSolid
4	Fill the map Same Domain solids myShapesSD	BOPAlgo_Builder::BuildSplitSolids()
5	Fill the map myImages	BOPAlgo_Builder::BuildSplitSolids()
6	Add internal vertices to split solids	BOPAlgo_Builder::FillInternalShapes()

Build Result of Type Solid

This step is the same as Building Result of Type Vertex, but for the type Solid.

Build Images for Type CompSolid

The input data for this step is:

BOPAlgo_Builder object after building result of type solid;
Original Shape – a Compsolid;
Type – the type of the shape (TopAbs_COMPSOLID).

The procedure is the same as for building images for wires.

Build Result of Type Compsolid

This step is the same as Building Result of Type Vertex, but for the type Compsolid.

Build Images for Compounds

The input data for this step is as follows:

BOPAlgo_Builder object after building results of type compsolid;
Original Shape – a Compound;
Type – the type of the shape (TopAbs_COMPOUND).

The procedure is the same as for building images for wires.

Build Result of Type Compound

This step is the same as Building Result of Type Vertex, but for the type Compound.

Post-Processing

The purpose of the step is to correct tolerances of the result to provide its validity in terms of BRepCheck_Analyzer.

The input data for this step is a BOPAlgo_Builder object after building result of type compound.

No	Contents	Implementation
1	Correct tolerances of vertices on curves	BOPTools_Tools::CorrectPointOnCurve()
2	Correct tolerances of edges on faces	BOPTools_Tools::CorrectCurveOnSurface()

Splitter Algorithm

The Splitter algorithm allows splitting a group of arbitrary shapes by another group of arbitrary shapes.
It is based on the General Fuse algorithm, thus all options of the General Fuse such as Fuzzy mode, safe processing mode, parallel mode, gluing mode and history support are also available in this algorithm.

Arguments

The arguments of the Splitter algorithm are divided into two groups - Objects (shapes that will be split) and Tools (shapes, by which the Objects will be split);
The requirements for the arguments (both for Objects and Tools) are the same as for the General Fuse algorithm - there can be any number of arguments of any type in each group, but each argument should be valid and not self-interfered.

Results

The result of Splitter algorithm contains only the split parts of the shapes included into the group of Objects;
The split parts of the shapes included only into the group of Tools are excluded from the result;
If there are no shapes in the group of Tools the result of the operation will be equivalent to the result of General Fuse operation;
The shapes can be split by other shapes from the same group (if these shapes are interfering).

Usage

API

On the low level the Splitter algorithm is implemented in class BOPAlgo_Splitter. The usage of this algorithm looks as follows:

BOPAlgo_Splitter aSplitter;
BOPCol_ListOfShape aLSObjects = …; // Objects
BOPCol_ListOfShape aLSTools = …; // Tools
Standard_Boolean bRunParallel = Standard_False; /* parallel or single mode (the default value is FALSE)*/
Standard_Real aTol = 0.0; /* fuzzy option (default value is 0)*/
Standard_Boolean bSafeMode = Standard_False; /* protect or not the arguments from modification*/
BOPAlgo_Glue aGlue = BOPAlgo_GlueOff; /* Glue option to speed up intersection of the arguments*/
// setting arguments
aSplitter.SetArguments(aLSObjects);
aSplitter.SetTools(aLSTools);
// setting options
aSplitter.SetRunParallel(bRunParallel);
aSplitter.SetFuzzyValue(aTol);
aSplitter.SetNonDestructive(bSafeMode);
aSplitter.SetGlue(aGlue);
//
aSplitter.Perform(); //perform the operation
if (aSplitter.HasErrors()) { //check error status
  return;
}
//
const TopoDS_Shape& aResult = aSplitter.Shape(); // result of the operation

DRAW

The command bsplit implements the Splitter algorithm in DRAW. Similarly to the bbuild command for the General Fuse algorithm, the bsplit command should be used after the Pave Filler is filled.

# s1 s2 s3 - objects
# t1 t2 t3 - tools
bclearobjects
bcleartools
baddobjects s1 s2 s3
baddtools t1 t2 t3
bfillds
bsplit result

Examples

Example 1

Splitting a face by the set of edges:

# draw script for reproducing
bclearobjects
bcleartools
set height 20
cylinder cyl 0 0 0 0 0 1 10
mkface f cyl 0 2*pi -$height $height
baddobjects f
# create tool edges
compound edges
set nb_uedges 10
set pi2 [dval 2*pi]
set ustep [expr $pi2/$nb_uedges]
for {set i 0} {$i <= $pi2} {set i [expr $i + $ustep]} {
  uiso c cyl $i
  mkedge e c -25 25
  add e edges
}
set nb_vedges 10
set vstep [expr 2*$height/$nb_vedges]
for {set i -20} {$i <= 20} {set i [expr $i + $vstep]} {
  viso c cyl $i
  mkedge e c
  add e edges
}
baddctools edges
bfillds
bsplit result

Arguments

Result

Example 2

Splitting a plate by the set of cylinders:

# draw script for reproducing:
bclearobjects
bcleartools
box plate 100 100 1
baddobjects plate
pcylinder p 1 11
compound cylinders
for {set i 0} {$i < 101} {incr i 5} {
  for {set j 0} {$j < 101} {incr j 5} {
    copy p p1;
    ttranslate p1 $i $j -5;
    add p1 cylinders
  }
}
baddtools cylinders
bfillds
bsplit result

Arguments

Result

Example 3

Splitting shell hull by the planes:

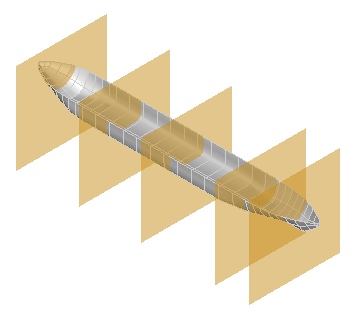
Arguments

Results

Boolean Operations Algorithm

Arguments

The arguments of BOA are shapes in terms of TopoDS_Shape. The main requirements for the arguments are described in the Data Structure
There are two groups of arguments in BOA:
- Objects (S1=S11, S12, ...);
- Tools (S2=S21, S22, ...).
The following table contains the values of dimension for different types of arguments:

No	Type of Argument	Index of Type	Dimension
1	COMPOUND	0	One of 0, 1, 2, 3
2	COMPSOLID	1	3
3	SOLID	2	3
4	SHELL	3	2
5	FACE	4	2
6	WIRE	5	1
7	EDGE	6	1
8	VERTEX	7	0

For Boolean operation Fuse all arguments should have equal dimensions.
For Boolean operation Cut the minimal dimension of S2 should not be less than the maximal dimension of S1.
For Boolean operation Common the arguments can have any dimension.

Results. General Rules

The result of the Boolean operation is a compound (if defined). Each sub-shape of the compound has shared sub-shapes in accordance with interferences between the arguments.
The content of the result depends on the type of the operation (Common, Fuse, Cut12, Cut21) and the dimensions of the arguments.
The result of the operation Fuse is defined for arguments S1 and S2 that have the same dimension value : Dim(S1)=Dim(S2). If the arguments have different dimension values the result of the operation Fuse is not defined. The dimension of the result is equal to the dimension of the arguments. For example, it is impossible to fuse an edge and a face.
The result of the operation Fuse for arguments S1 and S2 contains the parts of arguments that have states OUT relative to the opposite arguments.
The result of the operation Fuse for arguments S1 and S2 having dimension value 3 (Solids) is refined by removing all possible internal faces to provide minimal number of solids.
The result of the operation Common for arguments S1 and S2 is defined for all values of the dimensions of the arguments. The result can contain shapes of different dimensions, but the minimal dimension of the result will be equal to the minimal dimension of the arguments. For example, the result of the operation Common between edges cannot be a vertex.
The result of the operation Common for the arguments S1 and S2 contains the parts of the argument that have states IN and ON relative to the opposite argument.
The result of the operation Cut is defined for arguments S1 and S2 that have values of dimensions Dim(S2) that should not be less than Dim(S1). The result can contain shapes of different dimensions, but the minimal dimension of the result will be equal to the minimal dimension of the objects Dim(S1). The result of the operation Cut12 is not defined for other cases. For example, it is impossible to cut an edge from a solid, because a solid without an edge is not defined.
The result of the operation Cut12 for arguments S1 and S2 contains the parts of argument S1 that have state OUT relative to the opposite argument S2.
The result of the operation Cut21 for arguments S1 and S2 contains the parts of argument S2 that have state OUT relative to the opposite argument S1.
For the arguments of collection type (WIRE, SHELL, COMPSOLID) the type will be passed in the result. For example, the result of Common operation between Shell and Wire will be a compound containing Wire.
For the arguments of collection type (WIRE, SHELL, COMPSOLID) containing overlapping parts the overlapping parts passed into result will be repeated for each container from the input shapes containing such parts. The containers completely included in other containers will be avoided in the result.
For the arguments of collection type (WIRE, SHELL, COMPSOLID) the containers included into result will have the same orientation as the original containers from arguments. In case of duplication its orientation will be defined by the orientation of the first container in arguments. Each container included into result will have coherent orientation of its sub-shapes.
The result of the operation Fuse for the arguments of collection type (WIRE, SHELL) will consist of the shapes of the same collection type. The overlapping parts (EDGES/FACES) will be shared among containers, but duplicating containers will be avoided in the result. For example, the result of Fuse operation between two fully coinciding wires will be one wire, but the result of Fuse operation between two partially coinciding wires will be two wires sharing coinciding edges.
The result of the operation Fuse for the arguments of type COMPSOLID will consist of the compound containing COMPSOLIDs created from connexity blocks of fused solids.
The result of the operation Common for the arguments of collection type (WIRE, SHELL, COMPSOLID) will consist of the unique containers containing the overlapping parts. For example, the result of Common operation between two fully overlapping wires will be one wire containing all splits of edges. The number of wires in the result of Common operation between two partially overlapping wires will be equal to the number of connexity blocks of overlapping edges.

Examples

Case 1: Two Vertices

Let us consider two interfering vertices V1 and V2:

boolean_image001.svg

The result of Fuse operation is the compound that contains new vertex V.

boolean_image002.svg

The result of Common operation is a compound containing new vertex V.
The result of Cut12 operation is an empty compound.
The result of Cut21 operation is an empty compound.

Case 2: A Vertex and an Edge

Let us consider vertex V1 and the edge E2, that intersect in a 3D point:

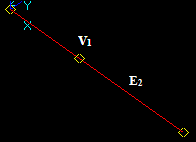
The result of Fuse operation is result is not defined because the dimension of the vertex (0) is not equal to the dimension of the edge (1).
The result of Common operation is a compound containing vertex V₁ as the argument V₁ has a common part with edge E2.

The result of Cut12 operation is an empty compound.
The result of Cut21 operation is not defined because the dimension of the vertex (0) is less than the dimension of the edge (1).

Case 3: A Vertex and a Face

Let us consider vertex V1 and face F2, that intersect in a 3D point:

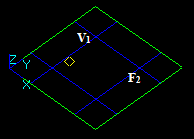
The result of Fuse operation is not defined because the dimension of the vertex (0) is not equal to the dimension of the face (2).
The result of Common operation is a compound containing vertex V₁ as the argument V₁ has a common part with face F2.

The result of Cut12 operation is an empty compound.
The result of Cut21 operation is not defined because the dimension of the vertex (0) is less than the dimension of the face (2).

Case 4: A Vertex and a Solid

Let us consider vertex V1 and solid S2, that intersect in a 3D point:

The result of Fuse operation is not defined because the dimension of the vertex (0) is not equal to the dimension of the solid (3).
The result of Common operation is a compound containing vertex V₁ as the argument V₁ has a common part with solid S2.

The result of Cut12 operation is an empty compound.
The result of Cut21 operation is not defined because the dimension of the vertex (0) is less than the dimension of the solid (3).

Case 5: Two edges intersecting at one point

Let us consider edges E1 and E2 that intersect in a 3D point:

boolean_image010.svg

The result of Fuse operation is a compound containing split parts of arguments i.e. 4 new edges E11, E12, E21, and E22. These edges have one shared vertex Vn1. In this case:
- argument edge E1 has resulting split edges E11 and E12 (image of E1);
- argument edge E2 has resulting split edges E21 and E22 (image of E2).

boolean_image011.svg

The result of Common operation is an empty compound because the dimension (0) of the common part between the edges (vertex) is less than the dimension of the arguments (1).
The result of Cut12 operation is a compound containing split parts of the argument E1, i.e. 2 new edges E11 and E12. These edges have one shared vertex Vn1.

In this case the argument edge E1 has resulting split edges E11 and E12 (image of E1).

boolean_image012.svg

The result of Cut21 operation is a compound containing split parts of the argument E2, i.e. 2 new edges E21 and E12. These edges have one shared vertex Vn1.

In this case the argument edge E2 has resulting split edges E21 and E22 (image of E2).

boolean_image013.svg

Case 6: Two edges having a common block

Let us consider edges E1 and E2 that have a common block:

boolean_image014.svg

The result of Fuse operation is a compound containing split parts of arguments i.e. 3 new edges E11, E12 and E22. These edges have two shared vertices. In this case:
- argument edge E1 has resulting split edges E11 and E12 (image of E1);
- argument edge E2 has resulting split edges E21 and E22 (image of E2);
- edge E12 is common for the images of E1 and E2.

boolean_image015.svg

The result of Common operation is a compound containing split parts of arguments i.e. 1 new edge E12. In this case edge E12 is common for the images of E1 and E2. The common part between the edges (edge) has the same dimension (1) as the dimension of the arguments (1).

boolean_image016.svg

The result of Cut12 operation is a compound containing a split part of argument E1, i.e. new edge E11.

boolean_image017.svg

The result of Cut21 operation is a compound containing a split part of argument E2, i.e. new edge E22.

boolean_image018.svg

Case 7: An Edge and a Face intersecting at a point

Let us consider edge E1 and face F2 that intersect at a 3D point:

The result of Fuse operation is not defined because the dimension of the edge (1) is not equal to the dimension of the face (2).
The result of Common operation is an empty compound because the dimension (0) of the common part between the edge and face (vertex) is less than the dimension of the arguments (1).
The result of Cut12 operation is a compound containing split parts of the argument E1, i.e. 2 new edges E11 and E12.

In this case the argument edge E1 has no common parts with the face F2 so the whole image of E1 is in the result.

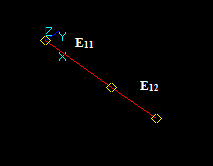
The result of Cut21 operation is not defined because the dimension of the edge (1) is less than the dimension of the face (2).

Case 8: A Face and an Edge that have a common block

Let us consider edge E1 and face F2 that have a common block:

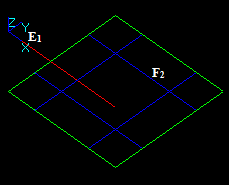
The result of Fuse operation is not defined because the dimension of the edge (1) is not equal to the dimension of the face (2).
The result of Common operation is a compound containing a split part of the argument E1, i.e. new edge E12.

In this case the argument edge E1 has a common part with face F2 so the corresponding part of the image of E1 is in the result. The yellow square is not a part of the result. It only shows the place of F2.

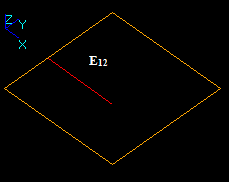
The result of Cut12 operation is a compound containing split part of the argument E1, i.e. new edge E11.

In this case the argument edge E1 has a common part with face F2 so the corresponding part is not included into the result. The yellow square is not a part of the result. It only shows the place of F2.

The result of Cut21 operation is not defined because the dimension of the edge (1) is less than the dimension of the face (2).

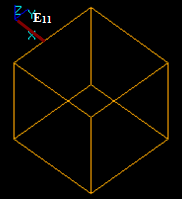
Case 9: An Edge and a Solid intersecting at a point

Let us consider edge E1 and solid S2 that intersect at a point:

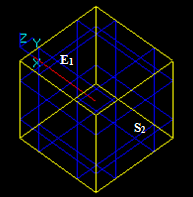
The result of Fuse operation is not defined because the dimension of the edge (1) is not equal to the dimension of the solid (3).
The result of Common operation is a compound containing a split part of the argument E1, i.e. new edge E12.

In this case the argument edge E1 has a common part with solid S2 so the corresponding part of the image of E1 is in the result. The yellow square is not a part of the result. It only shows the place of S2.

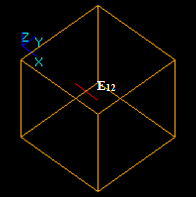
The result of Cut12 operation is a compound containing split part of the argument E1, i.e. new edge E11.

In this case the argument edge E1 has a common part with solid S2 so the corresponding part is not included into the result. The yellow square is not a part of the result. It only shows the place of S2.

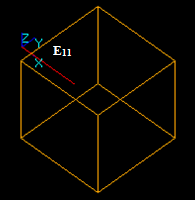
The result of Cut21 operation is not defined because the dimension of the edge (1) is less than the dimension of the solid (3).

Case 10: An Edge and a Solid that have a common block

Let us consider edge E1 and solid S2 that have a common block:

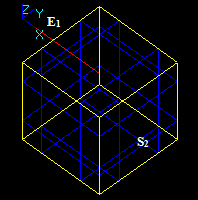
The result of Fuse operation is not defined because the dimension of the edge (1) is not equal to the dimension of the solid (3).
The result of Common operation is a compound containing a split part of the argument E1, i.e. new edge E12.

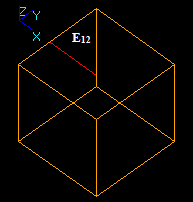
The result of Cut12 operation is a compound containing split part of the argument E1, i.e. new edge E11.

The result of Cut21 operation is not defined because the dimension of the edge (1) is less than the dimension of the solid (3).

Case 11: Two intersecting faces

Let us consider two intersecting faces F1 and F2:

The result of Fuse operation is a compound containing split parts of arguments i.e. 2 new faces F11 and F21. These faces have one shared edge En1.

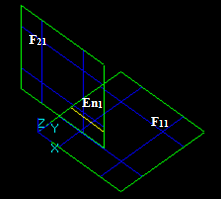
The result of Common operation is an empty compound because the dimension (1) of the common part between F1 and F2 (edge) is less than the dimension of arguments (2).
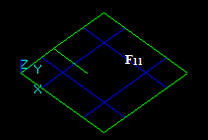
The result of Cut12 operation is a compound containing split part of the argument F1, i.e. new face F11.

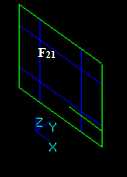
The result of Cut21 operation is a compound containing split parts of the argument F2, i.e. 1 new face F21.

Case 12: Two faces that have a common part

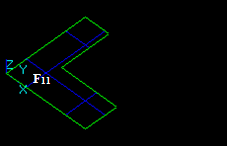
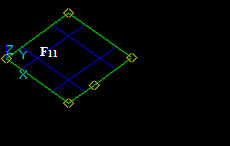
Let us consider two faces F1 and F2 that have a common part:

The result of Fuse operation is a compound containing split parts of arguments, i.e. 3 new faces: F11, F12 and F22. These faces are shared through edges In this case:
- the argument edge F1 has resulting split faces F11 and F12 (image of F1)
- the argument face F2 has resulting split faces F12 and F22 (image of F2)
- the face F12 is common for the images of F1 and F2.

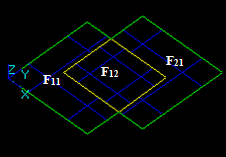
The result of Common operation is a compound containing split parts of arguments i.e. 1 new face F12. In this case: face F12 is common for the images of F1 and F2. The common part between the faces (face) has the same dimension (2) as the dimension of the arguments (2).

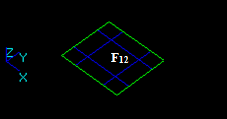
The result of Cut12 operation is a compound containing split part of the argument F1, i.e. new face F11.

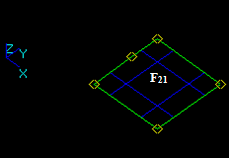
The result of Cut21 operation is a compound containing split parts of the argument F2, i.e. 1 new face F21.

Case 13: Two faces that have a common edge

Let us consider two faces F1 and F2 that have a common edge:

The result of Fuse operation is a compound containing split parts of arguments, i.e. 2 new faces: F11 and F21. These faces have one shared edge En1.

The result of Common operation is an empty compound because the dimension (1) of the common part between F1 and F2 (edge)is less than the dimension of the arguments (2)
The result of Cut12 operation is a compound containing split part of the argument F1, i.e. new face F11. The vertices are shown just to clarify the fact that the edges are spitted.

The result of Cut21 operation is a compound containing split parts of the argument F2, i.e. 1 new face F21. The vertices are shown just to clarify the fact that the edges are spitted.

Case 14: Two faces that have a common vertex

Let us consider two faces F1 and F2 that have a common vertex:

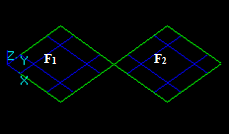
The result of Fuse operation is a compound containing split parts of arguments, i.e. 2 new faces: F11 and F21. These faces have one shared vertex Vn1.

The result of Common operation is an empty compound because the dimension (0) of the common part between F1 and F2 (vertex) is less than the dimension of the arguments (2)
The result of Cut12 operation is a compound containing split part of the argument F1, i.e. new face F11.

The result of Cut21 operation is a compound containing split parts of the argument F2, i.e. 1 new face F21.

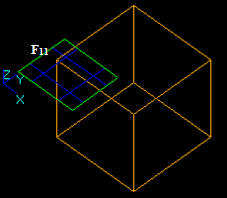
Case 15: A Face and a Solid that have an intersection curve.

Let us consider face F1 and solid S2 that have an intersection curve:

The result of Fuse operation is not defined because the dimension of the face (2) is not equal to the dimension of the solid (3).
The result of Common operation is a compound containing split part of the argument F1. In this case the argument face F1 has a common part with solid S2, so the corresponding part of the image of F1 is in the result. The yellow contour is not a part of the result. It only shows the place of S2.

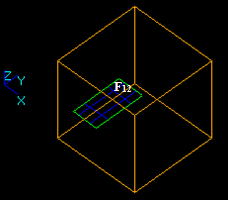
The result of Cut12 operation is a compound containing split part of the argument F1. In this case argument face F1 has a common part with solid S2 so the corresponding part is not included into the result. The yellow contour is not a part of the result. It only shows the place of S2.

The result of Cut21 operation is is not defined because the dimension of the face (2) is less than the dimension of the solid (3).

Case 16: A Face and a Solid that have overlapping faces.

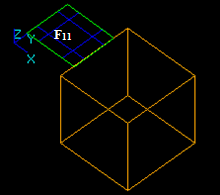
Let us consider face F1 and solid S2 that have overlapping faces:

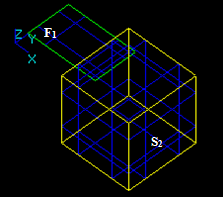
The result of Fuse operation is not defined because the dimension of the face (2) is not equal to the dimension of the solid (3).
The result of Common operation is a compound containing split part of the argument F1. In this case the argument face F1 has a common part with solid S2, so the corresponding part of the image of F1 is included in the result. The yellow contour is not a part of the result. It only shows the place of S2.

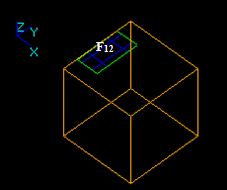
The result of Cut12 operation is a compound containing split part of the argument F1. In this case argument face F1 has a common part with solid S2 so the corresponding part is not included into the result. The yellow contour is not a part of the result. It only shows the place of S2.

The result of Cut21 operation is is not defined because the dimension of the face (2) is less than the dimension of the solid (3).

Case 17: A Face and a Solid that have overlapping edges.

Let us consider face F1 and solid S2 that have overlapping edges:

The result of Fuse operation is not defined because the dimension of the face (2) is not equal to the dimension of the solid (3).
The result of Common operation is an empty compound because the dimension (1) of the common part between F1 and S2 (edge) is less than the lower dimension of the arguments (2).
The result of Cut12 operation is a compound containing split part of the argument F1. In this case argument face F1 has a common part with solid S2 so the corresponding part is not included into the result. The yellow contour is not a part of the result. It only shows the place of S2.

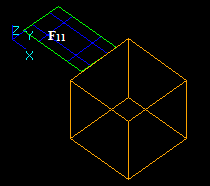
The result of Cut21 operation is is not defined because the dimension of the face (2) is less than the dimension of the solid (3).

Case 18: A Face and a Solid that have overlapping vertices.

Let us consider face F1 and solid S2 that have overlapping vertices:

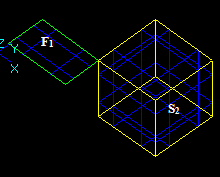
The result of Fuse operation is not defined because the dimension of the face (2) is not equal to the dimension of the solid (3).
The result of Common operation is an empty compound because the dimension (1) of the common part between F1 and S2 (vertex) is less than the lower dimension of the arguments (2).
The result of Cut12 operation is a compound containing split part of the argument F1. In this case argument face F1 has a common part with solid S2 so the corresponding part is not included into the result. The yellow contour is not a part of the result. It only shows the place of S2.

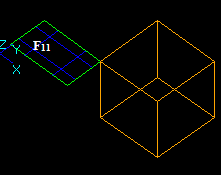
The result of Cut21 operation is is not defined because the dimension of the face (2) is less than the dimension of the solid (3).

Case 19: Two intersecting Solids.

Let us consider two intersecting solids S1 and S2:

The result of Fuse operation is a compound composed from the split parts of arguments S11, S12 and S22 (Cut12, Common, Cut21). All inner webs are removed, so the result is one new solid R.

The result of Common operation is a compound containing split parts of arguments i.e. one new solid S12. In this case solid S12 is common for the images of S1 and S2. The common part between the solids (solid) has the same dimension (3) as the dimension of the arguments (3). The yellow contour is not a part of the result. It only shows the place of S1.

The result of Cut12 operation is a compound containing split part of the argument S1, i.e. 1 new solid S11.

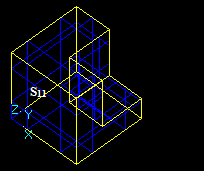
The result of Cut21 operation is a compound containing split part of the argument S2, i.e. 1 new solid S21.

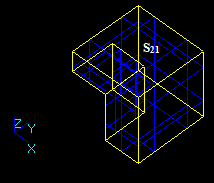
Case 20: Two Solids that have overlapping faces.

Let us consider two solids S1 and S2 that have a common part on face:

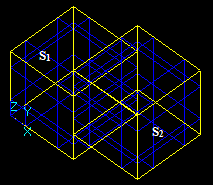
The result of Fuse operation is a compound composed from the split parts of arguments S11, S12 and S22 (Cut12, Common, Cut21). All inner webs are removed, so the result is one new solid R.

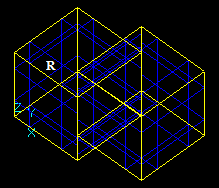
The result of Common operation is an empty compound because the dimension (2) of the common part between S1 and S2 (face) is less than the lower dimension of the arguments (3).
The result of Cut12 operation is a compound containing split part of the argument S1, i.e. 1 new solid S11.

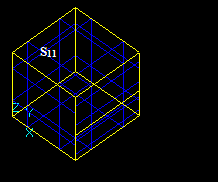
The result of Cut21 operation is a compound containing split part of the argument S2, i.e. 1 new solid S21.

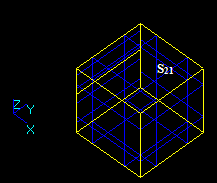
Case 21: Two Solids that have overlapping edges.

Let us consider two solids S1 and S2 that have overlapping edges:

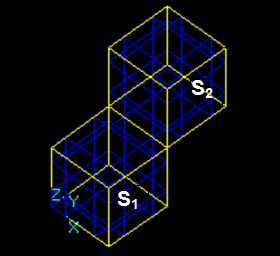
The result of Fuse operation is a compound composed from the split parts of arguments i.e. 2 new solids S11 and S21. These solids have one shared edge En1.

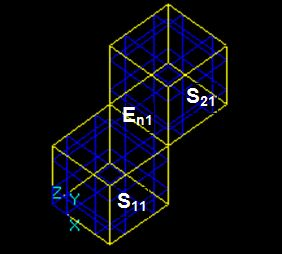
The result of Common operation is an empty compound because the dimension (1) of the common part between S1 and S2 (edge) is less than the lower dimension of the arguments (3).
The result of Cut12 operation is a compound containing split part of the argument S1. In this case argument S1 has a common part with solid S2 so the corresponding part is not included into the result.

The result of Cut21 operation is a compound containing split part of the argument S2. In this case argument S2 has a common part with solid S1 so the corresponding part is not included into the result.

Case 22: Two Solids that have overlapping vertices.

Let us consider two solids S1 and S2 that have overlapping vertices:

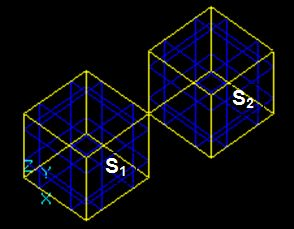
The result of Fuse operation is a compound composed from the split parts of arguments i.e. 2 new solids S11 and S21. These solids share Vn1.

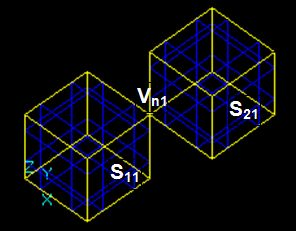
The result of Common operation is an empty compound because the dimension (0) of the common part between S1 and S2 (vertex) is less than the lower dimension of the arguments (3).
The result of Cut12 operation is a compound containing split part of the argument S1.

The result of Cut21 operation is a compound containing split part of the argument S2.

Case 23: A Shell and a Wire cut by a Solid.

Let us consider Shell Sh and Wire W as the objects and Solid S as the tool:

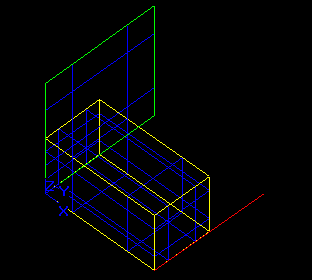
The result of Fuse operation is not defined as the dimension of the arguments is not the same.
The result of Common operation is a compound containing the parts of the initial Shell and Wire common for the Solid. The new Shell and Wire are created from the objects.

The result of Cut12 operation is a compound containing new Shell and Wire split from the arguments Sh and W. In this case they have a common part with solid S so the corresponding part is not included into the result.

The result of Cut21 operation is not defined as the objects have a lower dimension than the tool.

Case 24: Two Wires that have overlapping edges.

Let us consider two Wires that have overlapping edges, W1 is the object and W2 is the tool:

The result of Fuse operation is a compound containing two Wires, which share an overlapping edge. The new Wires are created from the objects:

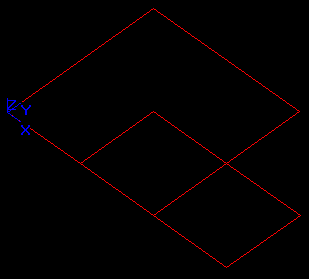
The result of Common operation is a compound containing one Wire consisting of an overlapping edge. The new Wire is created from the objects:

The result of Cut12 operation is a compound containing a wire split from object W1. Its common part with W2 is not included into the result.

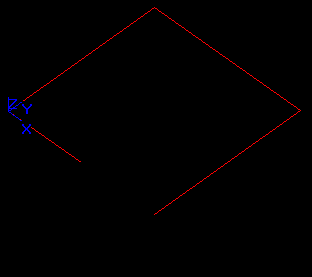
The result of Cut21 operation is a compound containing a wire split from W2. Its common part with W1 is not included into the result.

Class BOPAlgo_BOP

BOA is implemented in the class BOPAlgo_BOP. The main fields of this class are described in the Table:

Name	Contents
myOperation	The type of the Boolean operation (Common, Fuse, Cut)
myTools	The tools
myDims[2]	The values of the dimensions of the arguments
myRC	The draft result (shape)

The main steps of the BOPAlgo_BOP are the same as of BOPAlgo_Builder except for some aspects described in the next paragraphs.

Building Draft Result

The input data for this step is as follows:

BOPAlgo_BOP object after building result of type Compound;
Type of the Boolean operation.

No	Contents	Implementation
1	For the Boolean operation Fuse add to myRC all images of arguments.	BOPAlgo_BOP::BuildRC()
2	For the Boolean operation Common or Cut add to myRC all images of argument S1 that are Common for the Common operation and are Not Common for the Cut operation	BOPAlgo_BOP::BuildRC()

Building the Result

The input data for this step is as follows:

BOPAlgo_BOP object the state after building draft result.

No	Contents	Implementation
1	For the Type of the Boolean operation Common, Cut with any dimension and operation Fuse with myDim[0] < 3
1.1	Find containers (WIRE, SHELL, COMPSOLID) in the arguments	BOPAlgo_BOP:: BuildShape()
1.2	Make connexity blocks from splits of each container that are in myRC	BOPTools_Tools::MakeConnexityBlocks()
1.3	Build the result from shapes made from the connexity blocks	BOPAlgo_BOP:: BuildShape()
1.4	Add the remaining shapes from myRC to the result	BOPAlgo_BOP:: BuildShape()
2	For the Type of the Boolean operation Fuse with myDim[0] = 3
2.1	Find internal faces (FWi) in myRC	BOPAlgo_BOP::BuildSolid()
2.2	Collect all faces of myRC except for internal faces (FWi) -> SFS	BOPAlgo_BOP::BuildSolid ()
2.3	Build solids (SDi) from SFS.	BOPAlgo_BuilderSolid
2.4	Add the solids (SDi) to the result

Section Algorithm

Arguments

The arguments of BOA are shapes in terms of TopoDS_Shape. The main requirements for the arguments are described in the Algorithms.

Results and general rules

The result of Section operation is a compound. Each sub-shape of the compound has shared sub-shapes in accordance with interferences between the arguments.
The result of Section operation contains shapes that have dimension that is less then 2 i.e. vertices and edges.
The result of Section operation contains standalone vertices if these vertices do not belong to the edges of the result.
The result of Section operation contains vertices and edges of the arguments (or images of the arguments) that belong to at least two arguments (or two images of the arguments).
The result of Section operation contains Section vertices and edges obtained from Face/Face interferences.
The result of Section operation contains vertices that are the result of interferences between vertices and faces.
The result of Section operation contains edges that are the result of interferences between edges and faces (Common Blocks),

Examples

Case 1: Two Vertices

Let us consider two interfering vertices: V1 and V2.

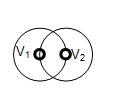
The result of Section operation is the compound that contains a new vertex V.

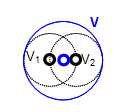
Case 1: Case 2: A Vertex and an Edge

Let us consider vertex V1 and the edge E2, that intersect in a 3D point:

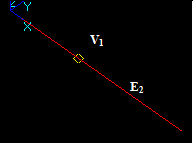
The result of Section operation is the compound that contains vertex V1.

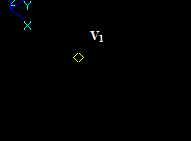
Case 1: Case 2: A Vertex and a Face

Let us consider vertex V1 and face F2, that intersect in a 3D point:

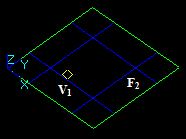
The result of Section operation is the compound that contains vertex V1.

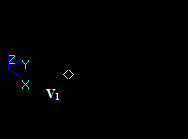
Case 4: A Vertex and a Solid

Let us consider vertex V1 and solid Z2. The vertex V1 is inside the solid Z2.

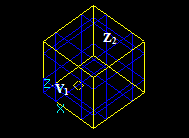
The result of Section operation is an empty compound.

Case 5: Two edges intersecting at one point

Let us consider edges E1 and E2, that intersect in a 3D point:

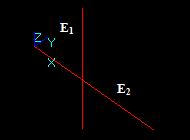
The result of Section operation is the compound that contains a new vertex Vnew.

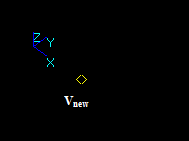
Case 6: Two edges having a common block

Let us consider edges E1 and E2, that have a common block:

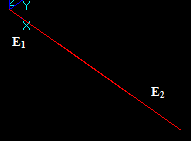
The result of Section operation is the compound that contains a new edge Enew.

Case 7: An Edge and a Face intersecting at a point

Let us consider edge E1 and face F2, that intersect at a 3D point:

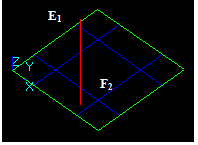
The result of Section operation is the compound that contains a new vertex Vnew.

Case 8: A Face and an Edge that have a common block

Let us consider edge E1 and face F2, that have a common block:

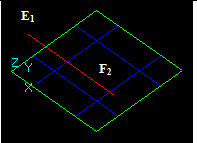
The result of Section operation is the compound that contains new edge Enew.

Case 9: An Edge and a Solid intersecting at a point

Let us consider edge E1 and solid Z2, that intersect at a point:

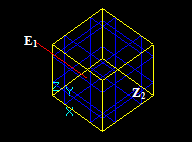
The result of Section operation is the compound that contains a new vertex Vnew.

Case 10: An Edge and a Solid that have a common block

Let us consider edge E1 and solid Z2, that have a common block at a face:

The result of Section operation is the compound that contains a new edge Enew.

Case 11: Two intersecting faces

Let us consider two intersecting faces F1 and F2:

The result of Section operation is the compound that contains a new edge Enew.

Case 12: Two faces that have a common part

Let us consider two faces F1 and F2 that have a common part:

The result of Section operation is the compound that contains 4 new edges.

Case 13: Two faces that have overlapping edges

Let us consider two faces F1 and F2 that have a overlapping edges:

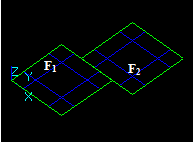
The result of Section operation is the compound that contains a new edge Enew.

Case 14: Two faces that have overlapping vertices

Let us consider two faces F1 and F2 that have overlapping vertices:

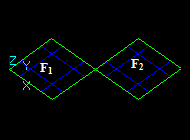
The result of Section operation is the compound that contains a new vertex Vnew.

Case 15: A Face and a Solid that have an intersection curve

Let us consider face F1 and solid Z2 that have an intersection curve:

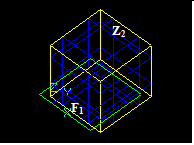
The result of Section operation is the compound that contains new edges.

Case 16: A Face and a Solid that have overlapping faces.

Let us consider face F1 and solid Z2 that have overlapping faces:

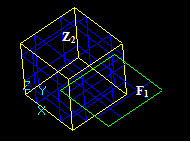
The result of Section operation is the compound that contains new edges

Case 17: A Face and a Solid that have overlapping edges.

Let us consider face F1 and solid Z2 that have a common part on edge:

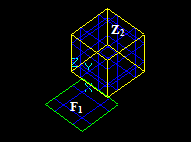
The result of Section operation is the compound that contains a new edge Enew.

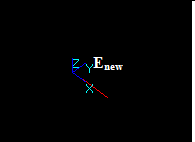
Case 18: A Face and a Solid that have overlapping vertices.

Let us consider face F1 and solid Z2 that have overlapping vertices:

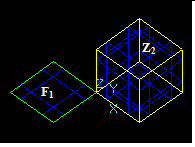
The result of Section operation is the compound that contains a new vertex Vnew.

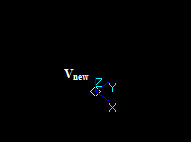
Case 19: Two intersecting Solids

Let us consider two intersecting solids Z1 and Z2:

The result of Section operation is the compound that contains new edges.

Case 20: Two Solids that have overlapping faces

Let us consider two solids Z1 and Z2 that have a common part on face:

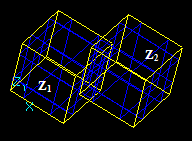
The result of Section operation is the compound that contains new edges.

Case 21: Two Solids that have overlapping edges

Let us consider two solids Z1 and Z2 that have overlapping edges:

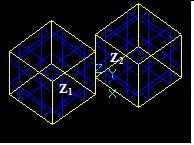
The result of Section operation is the compound that contains a new edge Enew.

Case 22: Two Solids that have overlapping vertices

Let us consider two solids Z1 and Z2 that have overlapping vertices:

The result of Section operation is the compound that contains a new vertex Vnew.

Class BOPAlgo_Section

SA is implemented in the class BOPAlgo_Section. The class has no specific fields. The main steps of the BOPAlgo_Section are the same as of BOPAlgo_Builder except for the following steps:

Build Images for Wires;
Build Result of Type Wire;
Build Images for Faces;
Build Result of Type Face;
Build Images for Shells;
Build Result of Type Shell;
Build Images for Solids;
Build Result of Type Solid;
Build Images for Type CompSolid;
Build Result of Type CompSolid;
Build Images for Compounds; Some aspects of building the result are described in the next paragraph

Building the Result

No	Contents	Implementation
1	Build the result of the operation using all information contained in FaceInfo, Common Block, Shared entities of the arguments, etc.	BOPAlgo_Section:: BuildSection()

Volume Maker Algorithm

The Volume Maker algorithm has been designed for building the elementary volumes (solids) from a set of connected, intersecting, or nested shapes. The algorithm can also be useful for splitting solids into parts, or constructing new solid(s) from set of intersecting or connected faces or shells. The algorithm creates only closed solids. In general case the result solids are non-manifold: fragments of the input shapes (wires, faces) located inside the solids are added as internal sub-shapes to these solids. But the algorithm allows preventing the addition of the internal for solids parts into result. In this case the result solids will be manifold and not contain any internal parts. However, this option does not prevent from the occurrence of the internal edges or vertices in the faces.
Non-closed faces, free wires etc. located outside of any solid are always excluded from the result.

The Volume Maker algorithm is implemented in the class BOPAlgo_MakerVolume. It is based on the General Fuse (GF) algorithm. All the options of the GF algorithm such as possibility to run algorithm in parallel mode, fuzzy option, safe mode, glue options and history support are also available in this algorithm.

The requirements for the arguments are the same as for the arguments of GF algorithm - they could be of any type, but each argument should be valid and not self-interfered.

The algorithm allows disabling the calculation of intersections among the arguments. In this case the algorithm will run much faster, but the user should guarantee that the arguments do not interfere with each other, otherwise the result will be invalid (e.g. contain unexpected parts) or empty. This option is useful e.g. for building a solid from the faces of one shell or from the shapes that have already been intersected.

Usage

C++ Level

The usage of the algorithm on the API level:

BOPAlgo_MakerVolume aMV;
BOPCol_ListOfShape aLS = …; // arguments
Standard_Boolean bRunParallel = Standard_False; /* parallel or single mode (the default value is FALSE)*/
Standard_Boolean bIntersect = Standard_True; /* intersect or not the arguments (the default value is TRUE)*/
Standard_Real aTol = 0.0; /* fuzzy option (default value is 0)*/
Standard_Boolean bSafeMode = Standard_False; /* protect or not the arguments from modification*/
BOPAlgo_Glue aGlue = BOPAlgo_GlueOff; /* Glue option to speed up intersection of the arguments*/
Standard_Boolean bAvoidInternalShapes = Standard_False; /* Avoid or not the internal for solids shapes in the result*/
//
aMV.SetArguments(aLS);
aMV.SetRunParallel(bRunParallel);
aMV.SetIntersect(bIntersect);
aMV.SetFuzzyValue(aTol);
aMV.SetNonDestructive(bSafeMode);
aMV.SetGlue(aGlue);
aMV.SetAvoidInternalShapes(bAvoidInternalShapes);
//
aMV.Perform(); //perform the operation
if (aMV.HasErrors()) { //check error status
  return;
}
//
const TopoDS_Shape& aResult = aMV.Shape(); // result of the operation

Tcl Level

To use the algorithm in Draw the command mkvolume has been implemented. The usage of this command is following:

Usage: mkvolume r b1 b2 ... [-c] [-ni] [-ai]
Options:
-c - use this option to have input compounds considered as set of separate arguments (allows passing multiple arguments as one compound);
-ni - use this option to disable the intersection of the arguments;
-ai - use this option to avoid internal for solids shapes in the result.

Examples

Example 1

Creation of 9832 solids from sphere and set of 63 planes:

Arguments

Results

Example 2

Creating compartments on a ship defined by hull shell and a set of planes. The ship is divided on compartments by five transverse bulkheads and a deck – six compartments are created:

Arguments

Results

Cells Builder algorithm

The Cells Builder algorithm is an extension of the General Fuse algorithm. The result of General Fuse algorithm contains all split parts of the arguments. The Cells Builder algorithm provides means to specify if any given split part of the arguments (referred to as Cell) can be taken or avoided in the result.

The possibility of selecting any Cell allows combining any possible result and gives the Cells Builder algorithm a very wide sphere of application - from building the result of any Boolean operation to building the result of any application-specific operation.

The algorithm builds Cells only once and then just reuses them for combining the result. This gives this algorithm the performance advantage over Boolean operations, which always rebuild the splits to obtain the desirable result.

Thus, the Cells Builder algorithm can be especially useful for simulating Boolean expressions, i.e. a sequence of Boolean operations on the same arguments. Instead of performing many Boolean operations it allows getting the final result in a single operation. The Cells Builder will also be beneficial to obtain the results of different Boolean operations on the same arguments - Cut and Common, for example.

The Cells Builder algorithm also provides the possibility to remove any internal boundaries between splits of the same type, i.e. to fuse any same-dimensional parts added into the result and to keep any other parts as separate. This possibility is implemented through the Cells material approach: to remove the boundary between two Cells, both Cells should be assigned with the same material ID. However, if the same material ID has been assigned to the Cells of different dimension, the removal of the internal boundaries for that material will not be performed. Currently, such case is considered a limitation for the algorithm.

The algorithm can also create containers from the connected Cells added into result - WIRES from Edges, SHELLS from Faces and COMPSOLIDS from Solids.

Usage

The algorithm has been implemented in the BOPAlgo_CellsBuilder class.

Cells Builder is based on the General Fuse algorithm. Thus all options of the General Fuse algorithm, such as parallel processing mode, fuzzy mode, safe processing mode, gluing mode and history support are also available in this algorithm.

The requirements for the input shapes are the same as for General Fuse - each argument should be valid in terms of BRepCheck_Analyzer and BOPAlgo_ArgumentAnalyzer.

The result of the algorithm is a compound containing the selected parts of the basic type (VERTEX, EDGE, FACE or SOLID). The default result is an empty compound. It is possible to add any Cell by using the methods AddToRessult() and AddAllToResult(). It is also possible to remove any part from the result by using methods RemoveFromResult() and RemoveAllFromResult(). The method RemoveAllFromResult() is also suitable for clearing the result.

The Cells that should be added/removed to/from the result are defined through the input shapes containing the parts that should be taken *(ShapesToTake)* and the ones containing parts that should be avoided (ShapesToAvoid). To be taken into the result the part must be IN all shapes from ShapesToTake and OUT of all shapes from ShapesToAvoid.

To remove Internal boundaries, it is necessary to set the same material to the Cells, between which the boundaries should be removed, and call the method RemoveInternalBoundaries(). The material should not be equal to 0, as this is the default material ID. The boundaries between Cells with this material ID will not be removed. The same Cell cannot be added with different materials. It is also possible to remove the boundaries when the result is combined. To do this, it is necessary to set the material for parts (not equal to 0) and set the flag bUpdate to TRUE. If the same material ID has been set for parts of different dimension, the removal of internal boundaries for this material will not be performed.

It is possible to create typed Containers from the parts added into result by using method MakeContainers(). The type of the containers will depend on the type of the input shapes: WIRES for EDGE, SHELLS for FACES and COMPSOLIDS for SOLIDS. The result will be a compound containing containers.

API usage

Here is the example of the algorithm use on the API level:

BOPAlgo_CellsBuilder aCBuilder;
BOPCol_ListOfShape aLS = …; // arguments
Standard_Boolean bRunParallel = Standard_False; /* parallel or single mode (the default value is FALSE)*/
Standard_Real aTol = 0.0; /* fuzzy option (the default value is 0)*/
Standard_Boolean bSafeMode = Standard_False; /* protect or not the arguments from modification*/
BOPAlgo_Glue aGlue = BOPAlgo_GlueOff; /* Glue option to speed up the intersection of arguments*/
//
aCBuilder.SetArguments(aLS);
aCBuilder.SetRunParallel(bRunParallel);
aCBuilder.SetFuzzyValue(aTol);
aCBuilder.SetNonDestructive(bSafeMode);
aCBuilder.SetGlue(aGlue);
//
aCBuilder.Perform(); // build splits of all arguments (GF)
if (aCBuilder.HasErrors()) { // check error status
  return;
}
//
// collecting of the cells into result
const TopoDS_Shape& anEmptyRes = aCBuilder.Shape(); // empty result, as nothing has been added yet 
const TopoDS_Shape& anAllCells = aCBuilder.GetAllParts(); //all split parts 
//
BOPCol_ListOfShape aLSToTake = ...; // parts of these arguments will be taken into result
BOPCol_ListOfShape aLSToAvoid = ...; // parts of these arguments will not be taken into result
//
Standard_Integer iMaterial = 1; // defines the material for the cells
Standard_Boolean bUpdate = Standard_False; // defines whether to update the result right now or not
// adding to result
aCBuilder.AddToResult(aLSToTake, aLSToAvoid, iMaterial, bUpdate);
aCBuilder.RemoveInternalBoundaries(); // removing of the boundaries
TopoDS_Shape aResult = aCBuilder.Shape(); // the result
// removing from result
aCBuilder.AddAllToResult();
aCBuilder.RemoveFromResult(aLSToTake, aLSToAvoid);
aResult = aCBuilder.Shape(); // the result

DRAW usage

The following set of new commands has been implemented to run the algorithm in DRAW Test Harness:

bcbuild          : Initialization of the Cells Builder. Use: *bcbuild r*
bcadd            : Add parts to result. Use: *bcadd r s1 (0,1) s2 (0,1) ... [-m material [-u]]*
bcaddall         : Add all parts to result. Use: *bcaddall r [-m material [-u]]*
bcremove         : Remove parts from result. Use: *bcremove r s1 (0,1) s2 (0,1) ...*
bcremoveall      : Remove all parts from result. Use: *bcremoveall*
bcremoveint      : Remove internal boundaries. Use: *bcremoveint r*
bcmakecontainers : Make containers from the parts added to result. Use: *bcmakecontainers r*

Here is the example of the algorithm use on the DRAW level:

psphere s1 15
psphere s2 15
psphere s3 15
ttranslate s1 0 0 10
ttranslate s2 20 0 10
ttranslate s3 10 0 0 
bclearobjects; bcleartools
baddobjects s1 s2 s3
bfillds
# rx will contain all split parts
bcbuild rx 
# add to result the part that is common for all three spheres
bcadd res s1 1 s2 1 s3 1 -m 1
# add to result the part that is common only for first and third spheres
bcadd res s1 1 s2 0 s3 1 -m 1
# remove internal boundaries
bcremoveint res

Examples

The following simple example illustrates the possibilities of the algorithm working on a cylinder and a sphere intersected by a plane:

pcylinder c 10 30 
psphere s 15
ttranslate s 0 0 30
plane p 0 0 20 1 0 0
mkface f p -25 30 -17 17

Arguments

bclearobjects
bcleartools
baddobjects c s f
bfillds
bcbuild r

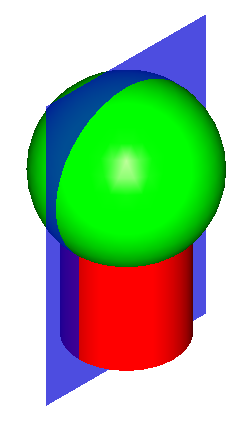
1. Common for all arguments

bcremoveall

bcadd res c 1 s 1 f 1

The result of COMMON operation

2. Common between cylinder and face

bcremoveall

bcadd res f 1 c 1

The result of COMMON operation between cylinder and face

3. Common between cylinder and sphere

bcremoveall

bcadd res c 1 s 1

The result of COMMON operation between cylinder and sphere

4. Fuse of cylinder and sphere

bcremoveall
bcadd res c 1 -m 1
bcadd res s 1 -m 1
bcremoveint res

The result of FUSE operation between cylinder and sphere

5. Parts of the face inside solids - FUSE(COMMON(f, c), COMMON(f, s))

bcremoveall
bcadd res f 1 s 1 -m 1
bcadd res f 1 c 1 -m 1

Parts of the face inside solids

bcremoveint res

Unified parts of the face inside solids

6. Part of the face outside solids

bcremoveall

bcadd res f 1 c 0 s 0

Part of the face outside solids

7. Fuse operation (impossible using standard Boolean Fuse operation)

bcremoveall
bcadd res c 1 -m 1
bcadd res s 1 -m 1
bcadd res f 1 c 0 s 0
bcremoveint res

Fuse operation

These examples may last forever. To define any new operation, it is just necessary to define, which Cells should be taken and which should be avoided.

Algorithm Limitations

The chapter describes the problems that are considered as Algorithm limitations. In most cases an Algorithm failure is caused by a combination of various factors, such as self-interfered arguments, inappropriate or ungrounded values of the argument tolerances, adverse mutual position of the arguments, tangency, etc.

A lot of failures of GFA algorithm can be caused by bugs in low-level algorithms: Intersection Algorithm, Projection Algorithm, Approximation Algorithm, Classification Algorithm, etc.

The Intersection, Projection and Approximation Algorithms are mostly used at the Intersection step. Their bugs directly cause wrong section results (i.e. incorrect section edges, section points, missing section edges or micro edges). It is not possible to obtain a correct final result of the GFA if a section result is wrong.
The Projection Algorithm is used at the Intersection step. The purpose of Projection Algorithm is to compute 2D curves on surfaces. Wrong results here lead to incorrect or missing faces in the final GFA result.
The Classification Algorithm is used at the Building step. The bugs in the Classification Algorithm lead to errors in selecting shape parts (edges, faces, solids) and ultimately to a wrong final GFA result.

The description below illustrates some known GFA limitations. It does not enumerate exhaustively all problems that can arise in practice. Please, address cases of Algorithm failure to the OCCT Maintenance Service.

Arguments

Common requirements

Each argument should be valid (in terms of BRepCheck_Analyzer), or conversely, if the argument is considered as non-valid (in terms of BRepCheck_Analyzer), it cannot be used as an argument of the algorithm.

The class BRepCheck_Analyzer is used to check the overall validity of a shape. In OCCT a Shape (or its sub-shapes) is considered valid if it meets certain criteria. If the shape is found as invalid, it can be fixed by tools from ShapeAnalysis, ShapeUpgrade and ShapeFix packages.

However, it is important to note that class BRepCheck_Analyzer is just a tool that can have its own problems; this means that due to a specific factor(s) this tool can sometimes provide a wrong result.

Let us consider the following example:

The Analyzer checks distances between couples of 3D check-points (Pi, PSi) of edge E on face F. Point Pi is obtained from the 3D curve (at the parameter ti) of the edge. PSi is obtained from 2D curve (at the parameter ti) of the edge on surface S of face F. To be valid the distance should be less than Tol(E) for all couples of check-points. The number of these check-points is a predefined value (e.g. 23).

Let us consider the case when edge E is recognized valid (in terms of BRepCheck_Analyzer).

Further, after some operation, edge E is split into two edges E1 and E2. Each split edge has the same 3D curve and 2D curve as the original edge E.

Let us check E1 (or E2). The Analyzer again checks the distances between the couples of check-points points (Pi, PSi). The number of these check-points is the same constant value (23), but there is no guarantee that the distances will be less than Tol(E), because the points chosen for E1 are not the same as for E.

Thus, if E1 is recognized by the Analyzer as non-valid, edge E should also be non-valid. However E has been recognized as valid. Thus the Analyzer gives a wrong result for E.

The fact that the argument is a valid shape (in terms of BRepCheck_Analyzer) is a necessary but insufficient requirement to produce a valid result of the Algorithms.

Pure self-interference

The argument should not be self-interfered, i.e. all sub-shapes of the argument that have geometrical coincidence through any topological entities (vertices, edges, faces) should share these entities.

Example 1: Compound of two edges

The compound of two edges E1 and E2 is a self-interfered shape and cannot be used as the argument of the Algorithms.

operations_image036.svg

Compound of two edges

Example 2: Self-interfered Edge

The edge E is a self-interfered shape and cannot be used as an argument of the Algorithms.

operations_image037.svg

Self-interfered Edge

Example 3: Self-interfered Face

The face F is a self-interfered shape and cannot be used as an argument of the Algorithms.

operations_image038.svg

Self-interfered Face

Example 4: Face of Revolution

The face F has been obtained by revolution of edge E around line L.

Face of Revolution: Arguments

Face of Revolution: Result

In spite of the fact that face F is valid (in terms of BRepCheck_Analyzer) it is a self-interfered shape and cannot be used as the argument of the Algorithms.

Self-interferences due to tolerances

Example 1: Non-closed Edge

Let us consider edge E based on a non-closed circle.

Edge based on a non-closed circle

The distance between the vertices of E is D=0.69799. The values of the tolerances Tol(V1)=Tol(V2)=0.5.

Distance and Tolerances

In spite of the fact that the edge E is valid in terms of BRepCheck_Analyzer, it is a self-interfered shape because its vertices are interfered. Thus, edge E cannot be used as an argument of the Algorithms.

Example 2: Solid containing an interfered vertex

Let us consider solid S containing vertex V.

Solid containing an interfered vertex

The value of tolerance Tol(V)= 50.000075982061.

Tolerance

In spite of the fact that solid S is valid in terms of BRepCheck_Analyzer it is a self-interfered shape because vertex V is interfered with a lot of sub-shapes from S without any topological connection with them. Thus solid S cannot be used as an argument of the Algorithms.

Parametric representation

The parameterization of some surfaces (cylinder, cone, surface of revolution) can be the cause of limitation.

Example 1: Cylindrical surface

The parameterization range for cylindrical surface is:

The range of U coordinate is always restricted while the range of V coordinate is non-restricted.

Let us consider a cylinder-based Face 1 with radii R=3 and H=6.

Face 1

P-Curves for Face 1

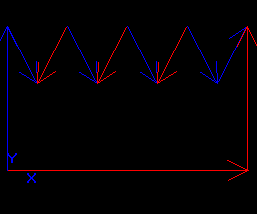
Let us also consider a cylinder-based Face 2 with radii R=3000 and H=6000 (resulting from scaling Face 1 with scale factor ScF=1000).

Face 2

P-Curves for Face 2

Please, pay attention to the Zoom value of the Figures.

It is obvious that starting with some value of ScF, e.g. ScF>1000000, all sloped p-Curves on Face 2 will be almost vertical. At least, there will be no difference between the values of angles computed by standard C Run-Time Library functions, such as double acos(double x). The loss of accuracy in computation of angles can cause failure of some BP sub-algorithms, such as building faces from a set of edges or building solids from a set of faces.

Using tolerances of vertices to fix gaps

It is possible to create shapes that use sub-shapes of lower order to avoid gaps in the tolerance-based data model.

Let us consider the following example:

Example

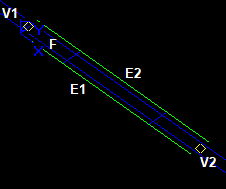
Face F has two edges E1 and E2 and two vertices, the base plane is {0,0,0, 0,0,1};
Edge E1 is based on line {0,0,0, 1,0,0}, Tol(E1) = 1.e-7;
Edge E2 is based on line {0,1,0, 1,0,0}, Tol(E2) = 1.e-7;
Vertex V1, point {0,0.5,0}, Tol(V1) = 1;
Vertex V2, point {10,0.5,0}, Tol(V2) = 1;
Face F is valid (in terms of BRepCheck_Analyzer).

The values of tolerances Tol(V1) and Tol(V2) are big enough to fix the gaps between the ends of the edges, but the vertices V1 and V2 do not contain any information about the trajectories connecting the corresponding ends of the edges. Thus, the trajectories are undefined. This will cause failure of some sub-algorithms of BP. For example, the sub-algorithms for building faces from a set of edges use the information about all edges connected in a vertex. The situation when a vertex has several pairs of edges such as above will not be solved in a right way.

Intersection problems

Pure intersections and common zones

Example: Intersecting Edges

Let us consider the intersection between two edges:

E1 is based on a line: {0,-10,0, 1,0,0}, Tol(E1)=2.
E2 is based on a circle: {0,0,0, 0,0,1}, R=10, Tol(E2)=2.

Intersecting Edges

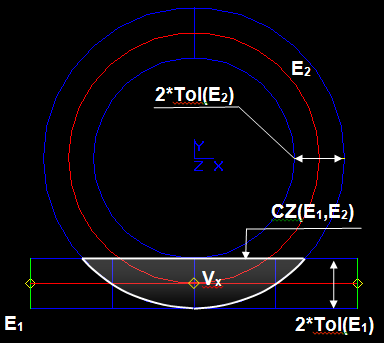
The result of pure intersection between E1 and E2 is vertex Vx {0,-10,0}.

The result of intersection taking into account tolerances is the common zone CZ (part of 3D-space where the distance between the curves is less than or equals to the sum of edge tolerances.

The Intersection Part of Algorithms uses the result of pure intersection Vx instead of CZ for the following reasons:

The Algorithms do not produce Common Blocks between edges based on underlying curves of explicitly different type (e.g. Line / Circle). If the curves have different types, the rule of thumb is that the produced result is of type vertex. This rule does not work for non-analytic curves (Bezier, B-Spline) and their combinations with analytic curves.
The algorithm of intersection between two surfaces IntPatch_Intersection does not compute CZ of the intersection between curves and points. So even if CZ were computed by Edge/Edge intersection algorithm, its result could not be treated by Face/Face intersection algorithm.

Tolerances and inaccuracies

The following limitations result from modeling errors or inaccuracies.

Example: Intersection of planar faces

Let us consider two planar rectangular faces F1 and F2.

The intersection curve between the planes is curve C12. The curve produces a new intersection edge EC12. The edge goes through vertices V1 and V2 thanks to big tolerance values of vertices Tol(V1) and Tol(V2). So, two straight edges E12 and EC12 go through two vertices, which is impossible in this case.

operations_image050.svg

Intersecting Faces

The problem cannot be solved in general, because the length of E12 can be infinite and the values of Tol(V1) and Tol(V2) theoretically can be infinite too.

In a particular case the problem can be solved in several ways:

Reduce, if possible, the values of Tol(V1) and Tol(V2) (refinement of F1).
Analyze the value of Tol(EC12) and increase Tol(EC12) to get a common part between the edges EC12 and E12. Then the common part will be rejected as there is an already existing edge E12 for face F1.

It is easy to see that if C12 is slightly above the tolerance spheres of V1 and V2 the problem does not appear.

Example: Intersection of two edges

Let us consider two edges E1 and E2, which have common vertices V1 and V2. The edges E1 and E2 have 3D-curves C1 and C2. Tol(E1)=1.e^-7, Tol(E2)=1.e^-7.

C1 practically coincides in 3D with C2. The value of deflection is Dmax (e.g. Dmax=1.e^-6).

operations_image051.svg

Intersecting Edges

The evident and prospective result should be the Common Block between E1 and E2. However, the result of intersection differs.

operations_image052.svg

Result of Intersection

The result contains three new vertices Vx1, Vx2 and Vx3, 8 new edges (V1, Vx1, Vx2, Vx3, V2) and no Common Blocks. This is correct due to the source data: Tol(E1)=1.e^-7, Tol(E2)=1.e^-7 and Dmax=1.e^-6.

In this particular case the problem can be solved by several ways:

Increase, if possible, the values Tol(E1) and Tol(E2) to get coincidence in 3D between E1 and E2 in terms of tolerance.
Replace E1 by a more accurate model.

The example can be extended from 1D (edges) to 2D (faces).

operations_image053.svg

Intersecting Faces

The comments and recommendations are the same as for 1D case above.

Acquired Self-interferences

Example 1: Vertex and edge

Let us consider vertex V1 and edge E2.

operations_image054.svg

Vertex and Edge

Vertex V1 interferes with vertices V12 and V22. So vertex V21 should interfere with vertex V22, which is impossible because vertices V21 and V22 are the vertices of edge E2, thus V21 is not equal to V22.

The problem cannot be solved in general, because the length can be as small as possible to provide validity of E2 (in the extreme case: Length (E2) = Tol(V21) + Tol(V22) + e, where e-> 0).

In a particular case the problem can be solved by refinement of arguments, i.e. by decreasing the values of Tol(V21), Tol(V22) and Tol(V1).

Example 2: Vertex and wire

Let us consider vertex V2 and wire consisting of edges E11 and E12.

operations_image055.svg

Vertex and Wire

The arguments themselves are not self-intersected. Vertex V2 interferes with edges E11 and E12. Thus, edge E11 should interfere with edge E22, but it is impossible because edges E11 and E12 cannot interfere by the condition.

The cases when a non-self-interfered argument (or its sub-shapes) become interfered due to the intersections with other arguments (or their sub-shapes) are considered as limitations for the Algorithms.

Advanced Options

The previous chapters describe so called Basic Operations. Most of tasks can be solved using Basic Operations. Nonetheless, there are cases that can not be solved straightforwardly by Basic Operations. The tasks are considered as limitations of Basic Operations.

The chapter is devoted to Advanced Options. In some cases the usage of Advanced Options allows overcoming the limitations, improving the quality of the result of operations, robustness and performance of the operators themselves.

Fuzzy Boolean Operation

Fuzzy Boolean operation is the option of Basic Operations such as General Fuse, Splitting, Boolean, Section, Maker Volume and Cells building operations, in which additional user-specified tolerance is used. This option allows operators to handle robustly cases of touching and near-coincident, misaligned entities of the arguments.

The Fuzzy option is useful on the shapes with gaps or embeddings between the entities of these shapes, which are not covered by the tolerance values of these entities. Such shapes can be the result of modeling mistakes, or translating process, or import from other systems with loss of precision, or errors in some algorithms.

Most likely, the Basic Operations will give unsatisfactory results on such models. The result may contain unexpected and unwanted small entities, faulty entities (in terms of BRepCheck_Analyzer), or there can be no result at all.

With the Fuzzy option it is possible to get the expected result – it is just necessary to define the appropriate value of fuzzy tolerance for the operation. To define that value it is necessary to measure the value of the gap (or the value of embedding depth) between the entities of the models, slightly increase it (to make the shifted entities coincident in terms of their tolerance plus the additional one) and pass it to the algorithm.

Fuzzy option is included in interface of Intersection Part (class BOPAlgo_PaveFiller) and application programming interface (class BRepAlgoAPI_BooleanOperation)

Examples

The following examples demonstrate the advantages of usage Fuzzy option operations over the Basic Operations in typical situations.

Case 1

In this example the cylinder (shown in yellow and transparent) is subtracted from the box (shown in red). The cylinder is shifted by 5e^-5 relatively to the box along its axis (the distance between rear faces of the box and cylinder is 5e^-5).

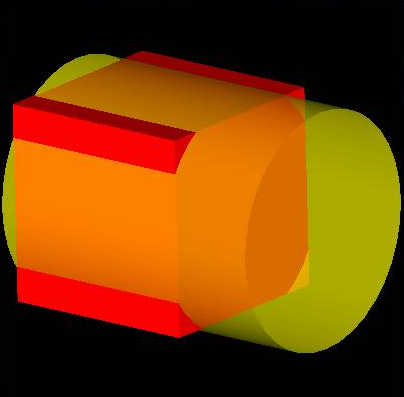
The following results are obtained using Basic Operations and the Fuzzy ones with the fuzzy value 5e^-5:

Result of CUT operation obtained with Basic Operations

Result of CUT operation obtained with Fuzzy Option

In this example Fuzzy option allows eliminating a very thin part of the result shape produced by Basic algorithm due to misalignment of rear faces of the box and the cylinder.

Case 2

In this example two boxes are fused. One of them has dimensions 10*10*10, and the other is 10*10.000001*10.000001 and adjacent to the first one. There is no gap in this case as the surfaces of the neighboring faces coincide, but one box is slightly greater than the other.

The following results are obtained using Basic Operations and the Fuzzy ones with the fuzzy value 1e^-6:

Result of CUT operation obtained with Basic Operations

Result of CUT operation obtained with Fuzzy Option

In this example Fuzzy option allows eliminating an extremely narrow face in the result produced by Basic operation.

Case 3

In this example the small planar face (shown in orange) is subtracted from the big one (shown in yellow). There is a gap 1e^-5 between the edges of these faces.

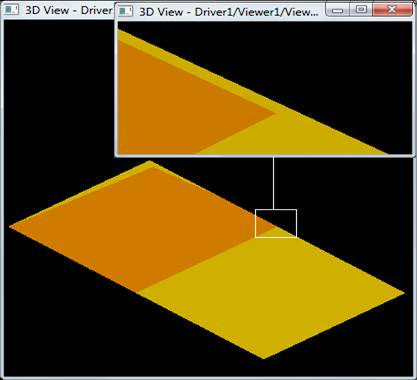
The following results are obtained using Basic Operations and the Fuzzy ones with the fuzzy value 1e^-5:

Result of CUT operation obtained with Basic Operations

Result of CUT operation obtained with Fuzzy Option

In this example Fuzzy options eliminated a pin-like protrusion resulting from the gap between edges of the argument faces.

Case 4

In this example the small edge is subtracted from the big one. The edges are overlapping not precisely, with max deviation between them equal to 5.28004e^-5. We will use 6e^-5 value for Fuzzy option.

The following results are obtained using Basic Operations and the Fuzzy ones with the fuzzy value 6e^-5:

Result of CUT operation obtained with Basic Operations

Result of CUT operation obtained with Fuzzy Option

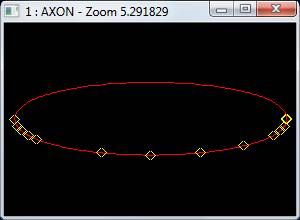
This example stresses not only the validity, but also the performance issue. The usage of Fuzzy option with the appropriate value allows processing the case much faster than with the pure Basic operation. The performance gain for the case is 45 (Processor: Intel(R) Core(TM) i5-3450 CPU @ 3.10 GHz).

Gluing Operation

The Gluing operation is the option of the Basic Operations such as General Fuse, Splitting, Boolean, Section, Maker Volume and Cells building operations. It has been designed to speed up the computation of the interferences among arguments of the operations on special cases, in which the arguments may be overlapping but do not have real intersections between their sub-shapes.

This option cannot be used on the shapes having real intersections, like intersection vertex between edges, or intersection vertex between edge and a face or intersection line between faces:

Intersecting faces

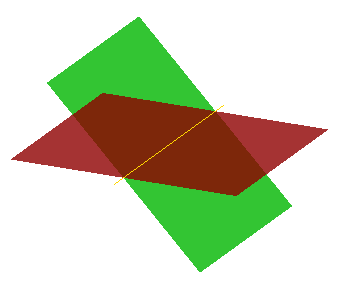
There are two possibilities of overlapping shapes:

The shapes can be partially coinciding - the faces do not have intersection curves, but overlapping. The faces of such arguments will be split during the operation. The following picture illustrates such shapes:

Partially coinciding faces

The shapes can be fully coinciding - there should be no partial overlapping of the faces, thus no intersection of type EDGE/FACE at all. In such cases the faces will not be split during the operation.

Full coinciding faces of the boxes

Thus, there are two possible options - for full and partial coincidence of the shapes.

Even though there are no real intersections on such cases without Gluing options the algorithm will still intersect the sub-shapes of the arguments with interfering bounding boxes.

The performance improvement in gluing mode is achieved by excluding the most time consuming computations and in some case can go up to 90%:

Exclude computation of FACE/FACE intersections for partial coincidence;
Exclude computation of VERTEX/FACE, EDGE/FACE and FACE/FACE intersections for full coincidence.

By setting the Gluing option for the operation user should guarantee that the arguments are really coinciding. The algorithm does not check this itself. Setting inappropriate option for the operation is likely to lead to incorrect result.

Usage

The Gluing option is an enumeration implemented in BOPAlgo_GlueEnum.hxx:

BOPAlgo_GlueOff - default value for the algorithms, Gluing is switched off;
BOPAlgo_GlueShift - Glue option for shapes with partial coincidence;
BOPAlgo_GlueFull - Glue option for shapes with full coincidence.

API level

For setting the Gluing options for the algorithm it is just necessary to call the SetGlue(const BOPAlgo_Glue) method with appropriate value:

BOPAlgo_Builder aGF;
//
....
// setting the gluing option to speed up intersection of the arguments
aGF.SetGlue(BOPAlgo_GlueShift)
//
....

TCL level

For setting the Gluing options in DRAW it is necessary to call the bglue command with appropriate value:

0 - default value, Gluing is off;
1 - for partial coincidence;
2 - for full coincidence

bglue 1

Examples

Case1 - Fusing the 64 bspline boxes into one solid

BSpline Boxes with partial coincidence

Performance improvement from using the GlueShift option in this case is about 70 percent.

Case2 - Sewing faces of the shape after reading from IGES

Faces with coinciding but not shared edges

Performance improvement in this case is also about 70 percent.

Safe processing mode

The safe processing mode is the advanced option in Boolean Operation component. This mode can be applied to all Basic operations such as General Fuse, Splitting, Boolean, Section, Maker Volume, Cells building. This option allows keeping the input arguments untouched. In other words, switching this option on prevents the input arguments from any modification such as tolerance increase, addition of the P-Curves on edges, etc.

The option can be very useful for implementation of the Undo/Redo mechanism in the applications and allows performing the operation many times without changing the inputs.

By default the safe processing option is switched off for the algorithms. Enabling this option might slightly decrease the performance of the operation, because instead of the modification of some entity it will be necessary to create the copy of this entity and modify it. However, this degradation should be very small because the copying is performed only in case of necessity.

The option is also available in the Intersection algorithm - BOPAlgo_PaveFiller. To perform several different operations on the same arguments, the safe processing mode can be enabled in PaveFiller, prepared only once and then used in operations. It is enough to set this option to PaveFiller only and all algorithms taking this PaveFiller will also work in the safe mode.

Usage

API level

To enable/disable the safe processing mode for the algorithm, it is necessary to call SetNonDestructive() method with the appropriate value:

BOPAlgo_Builder aGF;
//
....
// enabling the safe processing mode to prevent modification of the input shapes
aGF.SetNonDestructive(Standard_True);
//
....

TCL level

To enable the safe processing mode for the operation in DRAW, it is necessary to call the bnondestructive command with the appropriate value:

0 - default value, the safe mode is switched off;
1 - the safe mode will be switched on.

bnondestructive 1

Errors and warnings reporting system

The chapter describes the Error/Warning reporting system of the algorithms in the Boolean Component.

The errors and warnings are collected in the instance of the class Message_Report maintained as a field by common base class of Boolean operation algorithms BOPAlgo_Options.

The error is reported in for problems which cannot be treated and cause the algorithm to fail. In this case the result of the operation will be incorrect or incomplete or there will be no result at all.

The warnings are reported for the problems which can be potentially handled or ignored and thus do not cause the algorithms to stop their work (but probably affect the result).

All possible errors and warnings that can be set by the algorithm are listed in its header file. The complete list of errors and warnings that can be generated by Boolean operations is defined in BOPAlgo_Alerts.hxx.

Use method HasErrors() to check for presence of error; method HasError() can be used to check for particular error. Methods DumpErrors() outputs textual description of collected errors into the stream. Similar methods HasWarnings(), HasWarning(), and DumpWarnings() are provided for warnings.

Note that messages corresponding to errors and warnings are defined in resource file BOPAlgo.msg. These messages can be localized; for that put translated version to separate file and load it in the application by call to Message_MsgFile::Load() .

Here is the example of how to use this system:

BOPAlgo_PaveFiller aPF;
aPF.SetArguments(...);
aPF.Perform();
if (aPF.HasErrors()) {
  aPF.DumpErrors(std::cerr);
  //
  if (aPF.HasError(STANDARD_TYPE(BOPAlgo_AlertNullInputShapes)) {
    // some actions
  }
  if (aPF.HasWarning(STANDARD_TYPE(BOPAlgo_AlertTooSmallEdge)) {
    // some actions
  }
  ...
}

DRAW commands executing Boolean operations output errors and warnings generated by these operations in textual form. Additional option allows saving shapes for which warnings have been generated, as DRAW variables. To activate this option, run command bdrawwarnshapes with argument 1 (or with 0 to deactivate):

bdrawwarnshapes 1

After setting this option and running an algorithm the result will look as follows:

Warning: The interfering vertices of the same argument: ws_1_1 ws_1_2

Warning: The positioning of the shapes leads to creation of small edges without valid range: ws_2_1

Usage

The chapter contains some examples of the OCCT Boolean Component usage. The usage is possible on two levels: C++ and Tcl.

Package BRepAlgoAPI

The package BRepAlgoAPI provides the Application Programming Interface of the Boolean Component.

The package consists of the following classes:

BRepAlgoAPI_Algo – the root class that provides the interface for algorithms.
BRepAlgoAPI_BuilderAlgo – the class API level of General Fuse algorithm.
BRepAlgoAPI_Splitter – the class API level of the Splitter algorithm.
BRepAlgoAPI_BooleanOperation – the root class for the classes BRepAlgoAPI_Fuse. BRepAlgoAPI_Common, BRepAlgoAPI_Cut and BRepAlgoAPI_Section.
BRepAlgoAPI_Fuse – the class provides Boolean fusion operation.
BRepAlgoAPI_Common – the class provides Boolean common operation.
BRepAlgoAPI_Cut – the class provides Boolean cut operation.
BRepAlgoAPI_Section – the class provides Boolean section operation.

Diagram of BRepAlgoAPI package

The detailed description of the classes can be found in the corresponding .hxx files. The examples are below in this chapter.

Package BOPTest

The package BOPTest provides the usage of the Boolean Component on Tcl level. The method BOPTest::APICommands contains corresponding Tcl commands:

bapibuild – for General Fuse Operator;
bapisplit – for Splitter Operator;
bapibop – for Boolean Operator and Section Operator.

The examples of how to use the commands are below in this chapter.

Case 1. General Fuse operation

The following example illustrates how to use General Fuse operator:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include <BRepAlgoAPI_BuilderAlgo.hxx>
 {…
  Standard_Boolean bRunParallel;
  Standard_Real aFuzzyValue;
  BRepAlgoAPI_BuilderAlgo aBuilder;
  //
  // prepare the arguments
  TopTools_ListOfShape& aLS=…;
  //
  bRunParallel=Standard_True;
  aFuzzyValue=2.1e-5;
  //
  // set the arguments  
  aBuilder.SetArguments(aLS);
  // set parallel processing mode 
  // if  bRunParallel= Standard_True :  the parallel processing is switched on
  // if  bRunParallel= Standard_False :  the parallel processing is switched off
  aBuilder.SetRunParallel(bRunParallel);
  //
  // set Fuzzy value
  // if aFuzzyValue=0.: the Fuzzy option is off
  //  if aFuzzyValue>0.: the Fuzzy option is on
  aBuilder.SetFuzzyValue(aFuzzyValue);
  //
  // safe mode - avoid modification of the arguments
  Standard_Boolean bSafeMode = Standard_True;
  // if bSafeMode == Standard_True  - the safe mode is switched on
  // if bSafeMode == Standard_False - the safe mode is switched off
  aBuilder.SetNonDestructive(bSafeMode);
  //
  // gluing options - for coinciding arguments
  BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
  // if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
  // if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
  // if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
  aBuilder.SetGlue(aGlueOpt);
  //
  // run the algorithm 
  aBuilder.Build(); 
  if (aBuilder.HasErrors()) {
    // an error treatment
    return;
  }
  //
  // result of the operation aR
  const TopoDS_Shape& aR=aBuilder.Shape();
…
}

Tcl Level

# prepare the arguments
box b1 10 10 10 
box b2 3 4 5 10 10 10 
box b3 5 6 7 10 10 10 
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the arguments
baddobjects b1 b2 b3
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1 
#
# set Fuzzy value
# 0.    : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
#
# set gluing mode
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
bapibuild r 

Case 2. Splitting operation

The following example illustrates how to use the Splitter operator:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include <BRepAlgoAPI_Splitter.hxx>
//
BRepAlgoAPI_BuilderAlgo aSplitter;
//
// prepare the arguments
// objects
TopTools_ListOfShape& aLSObjects = … ;
// tools
TopTools_ListOfShape& aLSTools = … ;
//
// set the arguments
aSplitter.SetArguments(aLSObjects);
aSplitter.SetTools(aLSTools);
//
// set options
// parallel processing mode 
Standard_Boolean bRunParallel = Standard_True;
// bRunParallel == Standard_True  - the parallel processing is switched on
// bRunParallel == Standard_False - the parallel processing is switched off
aSplitter.SetRunParallel();
//
// fuzzy value - additional tolerance for the operation
Standard_Real aFuzzyValue = 1.e-5;
// if aFuzzyValue == 0. - the Fuzzy option is off
// if aFuzzyValue > 0.  - the Fuzzy option is on
aSplitter.SetFuzzyValue(aFuzzyValue);
//
// safe mode - avoid modification of the arguments
Standard_Boolean bSafeMode = Standard_True;
// if bSafeMode == Standard_True  - the safe mode is switched on
// if bSafeMode == Standard_False - the safe mode is switched off
aSplitter.SetNonDestructive(bSafeMode);
//
// gluing options - for coinciding arguments
BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
// if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
// if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
// if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
aSplitter.SetGlue(aGlueOpt);
//
// run the algorithm 
aSplitter.Build(); 
// check error status
if (aSplitter.HasErrors()) {
  return;
}
//
// result of the operation aResult
const TopoDS_Shape& aResult = aSplitter.Shape();

Tcl Level

# prepare the arguments
# objects
box b1 10 10 10 
box b2 7 0 0 10 10 10
# tools
plane p 10 5 5 0 1 0
mkface f p -20 20 -20 20
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the objects
baddobjects b1 b2
# set the tools
baddtools f
#
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1 
#
# set Fuzzy value
# 0.  : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
#
# set gluing mode
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
bapisplit r 

Case 3. Common operation

The following example illustrates how to use Common operation:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include < BRepAlgoAPI_Common.hxx>
 {…
  Standard_Boolean bRunParallel;
  Standard_Real aFuzzyValue;
  BRepAlgoAPI_Common aBuilder;
  // perpare the arguments
  TopTools_ListOfShape& aLS=…;
  TopTools_ListOfShape& aLT=…;
  //
  bRunParallel=Standard_True;
  aFuzzyValue=2.1e-5;
  //
  // set the arguments  
  aBuilder.SetArguments(aLS);
  aBuilder.SetTools(aLT);
  //    
  // set parallel processing mode 
  // if  bRunParallel= Standard_True :  the parallel processing is switched on
  // if  bRunParallel= Standard_False :  the parallel processing is switched off
  aBuilder.SetRunParallel(bRunParallel);
  //
  // set Fuzzy value
  // if aFuzzyValue=0.: the Fuzzy option is off
  //  if aFuzzyValue>0.: the Fuzzy option is on
  aBuilder.SetFuzzyValue(aFuzzyValue);
  //
  // safe mode - avoid modification of the arguments
  Standard_Boolean bSafeMode = Standard_True;
  // if bSafeMode == Standard_True  - the safe mode is switched on
  // if bSafeMode == Standard_False - the safe mode is switched off
  aBuilder.SetNonDestructive(bSafeMode);
  //
  // gluing options - for coinciding arguments
  BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
  // if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
  // if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
  // if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
  aBuilder.SetGlue(aGlueOpt);
  //
  // run the algorithm 
  aBuilder.Build(); 
  if (aBuilder.HasErrors()) {
    // an error treatment
    return;
  }
  //
  // result of the operation aR
  const TopoDS_Shape& aR=aBuilder.Shape();
…
}

Tcl Level

# prepare the arguments
box b1 10 10 10 
box b2 7 0 4 10 10 10 
box b3 14 0 0 10 10 10 
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the arguments
baddobjects b1 b3
baddtools b2
#
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1
#
# set Fuzzy value
# 0.    : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
#
# set gluing mode
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
# 0 means Common operation
bapibop r 0

Case 4. Fuse operation

The following example illustrates how to use Fuse operation:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include < BRepAlgoAPI_Fuse.hxx>
 {…
  Standard_Boolean bRunParallel;
  Standard_Real aFuzzyValue;
  BRepAlgoAPI_Fuse aBuilder;
  // perpare the arguments
  TopTools_ListOfShape& aLS=…;
  TopTools_ListOfShape& aLT=…;
  //
  bRunParallel=Standard_True;
  aFuzzyValue=2.1e-5;
  //
  // set the arguments  
  aBuilder.SetArguments(aLS);
  aBuilder.SetTools(aLT);
  //    
  // set parallel processing mode 
  // if  bRunParallel= Standard_True :  the parallel processing is switched on
  // if  bRunParallel= Standard_False :  the parallel processing is switched off
  aBuilder.SetRunParallel(bRunParallel);
  //
  // set Fuzzy value
  // if aFuzzyValue=0.: the Fuzzy option is off
  //  if aFuzzyValue>0.: the Fuzzy option is on
  aBuilder.SetFuzzyValue(aFuzzyValue);
  //
  // safe mode - avoid modification of the arguments
  Standard_Boolean bSafeMode = Standard_True;
  // if bSafeMode == Standard_True  - the safe mode is switched on
  // if bSafeMode == Standard_False - the safe mode is switched off
  aBuilder.SetNonDestructive(bSafeMode);
  //
  // gluing options - for coinciding arguments
  BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
  // if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
  // if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
  // if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
  aBuilder.SetGlue(aGlueOpt);
  //
  // run the algorithm 
  aBuilder.Build(); 
  if (aBuilder.HasErrors()) {
    // an error treatment
    return;
  }
  //
  // result of the operation aR
  const TopoDS_Shape& aR=aBuilder.Shape();
…
}

Tcl Level

# prepare the arguments
box b1 10 10 10 
box b2 7 0 4 10 10 10 
box b3 14 0 0 10 10 10 
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the arguments
baddobjects b1 b3
baddtools b2
#
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1
#
# set Fuzzy value
# 0.    : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
#
# set gluing mode
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
# 1 means Fuse operation
bapibop r 1

Case 5. Cut operation

The following example illustrates how to use Cut operation:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include < BRepAlgoAPI_Cut.hxx>
 {…
  Standard_Boolean bRunParallel;
  Standard_Real aFuzzyValue;
  BRepAlgoAPI_Cut aBuilder;
  // perpare the arguments
  TopTools_ListOfShape& aLS=…;
  TopTools_ListOfShape& aLT=…;
  //
  bRunParallel=Standard_True;
  aFuzzyValue=2.1e-5;
  //
  // set the arguments  
  aBuilder.SetArguments(aLS);
  aBuilder.SetTools(aLT);
  //    
  // set parallel processing mode 
  // if  bRunParallel= Standard_True :  the parallel processing is switched on
  // if  bRunParallel= Standard_False :  the parallel processing is switched off
  aBuilder.SetRunParallel(bRunParallel);
  //
  // set Fuzzy value
  // if aFuzzyValue=0.: the Fuzzy option is off
  //  if aFuzzyValue>0.: the Fuzzy option is on
  aBuilder.SetFuzzyValue(aFuzzyValue);
  //
  // safe mode - avoid modification of the arguments
  Standard_Boolean bSafeMode = Standard_True;
  // if bSafeMode == Standard_True  - the safe mode is switched on
  // if bSafeMode == Standard_False - the safe mode is switched off
  aBuilder.SetNonDestructive(bSafeMode);
  //
  // gluing options - for coinciding arguments
  BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
  // if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
  // if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
  // if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
  aBuilder.SetGlue(aGlueOpt);
  //
  // run the algorithm 
  aBuilder.Build(); 
  if (aBuilder.HasErrors()) {
    // an error treatment
    return;
  }
  //
  // result of the operation aR
  const TopoDS_Shape& aR=aBuilder.Shape();
…
}

Tcl Level

# prepare the arguments
box b1 10 10 10 
box b2 7 0 4 10 10 10 
box b3 14 0 0 10 10 10 
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the arguments
baddobjects b1 b3
baddtools b2
#
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1
#
# set Fuzzy value
# 0.    : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
# set gluing mode
#
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
# 2 means Cut operation
bapibop r 2

Case 6. Section operation

The following example illustrates how to use Section operation:

C++ Level

#include <TopoDS_Shape.hxx>
#include <TopTools_ListOfShape.hxx>
#include < BRepAlgoAPI_Section.hxx>
 {…
  Standard_Boolean bRunParallel;
  Standard_Real aFuzzyValue;
  BRepAlgoAPI_Section aBuilder;
  // perpare the arguments
  TopTools_ListOfShape& aLS=…;
  TopTools_ListOfShape& aLT=…;
  //
  bRunParallel=Standard_True;
  aFuzzyValue=2.1e-5;
  //
  // set the arguments  
  aBuilder.SetArguments(aLS);
  aBuilder.SetTools(aLT);
  //    
  // set parallel processing mode 
  // if  bRunParallel= Standard_True :  the parallel processing is switched on
  // if  bRunParallel= Standard_False :  the parallel processing is switched off
  aBuilder.SetRunParallel(bRunParallel);
  //
  // set Fuzzy value
  // if aFuzzyValue=0.: the Fuzzy option is off
  //  if aFuzzyValue>0.: the Fuzzy option is on
  aBuilder.SetFuzzyValue(aFuzzyValue);
  //
  // safe mode - avoid modification of the arguments
  Standard_Boolean bSafeMode = Standard_True;
  // if bSafeMode == Standard_True  - the safe mode is switched on
  // if bSafeMode == Standard_False - the safe mode is switched off
  aBuilder.SetNonDestructive(bSafeMode);
  //
  // gluing options - for coinciding arguments
  BOPAlgo_GlueEnum aGlueOpt = BOPAlgo_GlueFull;
  // if aGlueOpt == BOPAlgo_GlueOff   - the gluing mode is switched off
  // if aGlueOpt == BOPAlgo_GlueShift - the gluing mode is switched on
  // if aGlueOpt == BOPAlgo_GlueFull  - the gluing mode is switched on
  aBuilder.SetGlue(aGlueOpt);
  //
  // run the algorithm 
  aBuilder.Build(); 
  if (aBuilder.HasErrors()) {
    // an error treatment
    return;
  }
  //
  // result of the operation aR
  const TopoDS_Shape& aR=aBuilder.Shape();
…
}

Tcl Level

# prepare the arguments
box b1 10 10 10 
box b2 3 4 5 10 10 10 
box b3 5 6 7 10 10 10 
#
# clear inner contents
bclearobjects; bcleartools;
#
# set the arguments
baddobjects b1 b3
baddtools b2
#
# set parallel processing mode
# 1:  the parallel processing is switched on
# 0:  the parallel processing is switched off
brunparallel 1
#
# set Fuzzy value
# 0.    : the Fuzzy option is off
# >0. : the Fuzzy option is on
bfuzzyvalue 0.
#
# set safe processing mode
bnondestructive 1
# set safe mode
# 1 - the safe processing mode is switched on
# 0 - the safe processing mode is switched off
#
# set gluing mode
bglue 1
# set the gluing mode
# 1 or 2 - the gluing mode is switched on
# 0 - the gluing mode is switched off
#
# run the algorithm
# r is the result of the operation
# 4 means Section operation
bapibop r 4

Generated on Wed Aug 30 2017 17:04:21 for Open CASCADE Technology by

1.8.13

previous page start next page

Open CASCADE Technology: Boolean Operations

OpenCascade

Table of Contents

Introduction

Overview

Operators

Boolean operator

General Fuse operator

Splitter operator

Section operator

Parts of algorithms

Terms and Definitions

Interferences

Vertex/Vertex interference

Vertex/Edge interference

Vertex/Face interference

Edge/Edge interference

Edge/Face interference

Face/Face Interference

Vertex/Solid Interference

Edge/Soild Interference

Face/Soild Interference

Solid/Soild Interference

Computation Order

Results

Paves

Pave Blocks

Shrunk Range

Common Blocks

FaceInfo

Data Structure

Arguments

Shapes

Interferences

Pave, PaveBlock and CommonBlock

Points and Curves

FaceInfo

Root Classes

Class BOPAlgo_Options

Class BOPAlgo_Algo

Intersection Part

Initialization

Compute Vertex/Vertex Interferences

Compute Vertex/Edge Interferences

Update Pave Blocks

Compute Edge/Edge Interferences

Compute Vertex/Face Interferences

Compute Edge/Face Interferences

Build Split Edges

Compute Face/Face Interferences

Build Section Edges

Build P-Curves

Process Degenerated Edges

General description of the Building Part

General Fuse Algorithm

Arguments

Results

Examples

Case 1: Three edges intersecting at a point

Case 2: Two wires and an edge

Case 3: An edge intersecting with a face

Case 4: An edge lying on a face

Case 5: An edge and a shell

Case 6: A wire and a shell

Case 7: Three faces

Case 8: A face and a shell

Case 9: A shell and a solid

Case 10: A compound and a solid

Class BOPAlgo_Builder

Fields

Initialization

Build Images for Vertices

Build Result of Type Vertex

Build Images for Edges

Build Result of Type Edge

Build Images for Wires

Build Result of Type Wire

Build Images for Faces

Build Result of Type Face

Build Images for Shells