State-Space

Creates a single-input single-output (SISO) state-space model of a system using Matrix A, Matrix B, Matrix C, Matrix D, and the Sampling Time (s). This step also can produce a state-space model in which you can specify the data in symbolic form.

Details  

Parameter	Description
Name	Specifies the name of the model you create.
Inputs	Displays the number of inputs in the system model.
States	Displays the number of states in the system model.
Outputs	Displays the number of outputs in the system model.
Model Type	Specifies the type of model you create. Contains the following options: Continuous—Specifies that the model you create is in the continuous time domain. Discrete—Specifies that the model you create is in the discrete time domain. When you place a checkmark in the Discrete checkbox, the Sampling Time (s) parameter appears. Sampling Time (s)—Defines the sampling time used in the discrete model. The default is 1. By using the coefficients of the continuous model and setting the Sampling Time (s) of the system to a value greater than zero, you do not create the discrete-time equivalent of the system. If you create a continuous model and want to convert the model to a discrete model, you must use the Discretize Model step. If you already know the coefficients of a discrete transfer function model, you can create the model using this step. Enter the coefficients for the discrete model and set the Sampling Time (s) of the system to a value greater than zero.
Symbolic Coefficients	Specifies that you can use variables to define the model. Define the variable name and the value that the variable represents in the left and right columns, respectively, that appear in the Symbolic coefficients section. Number of Variables—Specifies the maximum number of variables used. The maximum number of variables you can specify is nine. Variables—Lists the coefficient variables and values. The number of variables you specify in the Number of Variables control corresponds to the number of rows in the Variables array.
Matrix A	Defines the system matrix that describes the dynamics of the states of the system.
Matrix B	Defines the input matrix that relates the inputs to the states of the system.
Matrix C	Defines the output matrix that relates the outputs to the state of the system.
Matrix D	Defines the transmission matrix that relates the inputs to the outputs of the systems.
Generate Random Model	Generates a random model.

State-Space Details

The state-space model is defined by the following equations:

Continuous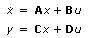
Discrete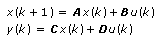

where k is the sampling time,

n is the number of states,

m is the number of inputs,

r is the number of outputs,

x is the state vector,

u is the input vector,

y is the output vector,

A is an n × n state matrix of the given system,

B is an n × m input matrix of the given system,

C is an r × n input matrix of the given system,

and D is an r × m input matrix of the given system.