PID Synthesis

Creates a controller based on changing the PID (proportional-integral-derivative) series algorithm as defined as below:

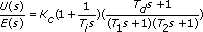
where K_c is the proportional gain,

T_i is the integral time in seconds,

and T_d is the derivative time in seconds.

T₁ is the HF Rolloff 1 time (in seconds), which defines the time constant of a first order filter in series with the PID algorithm.

T₂ is the HF Rolloff 2 time (in seconds), which defines the time constant of a first order filter in series with the PID algorithm.

Details  

Parameter	Description
Step Response	Displays the output of the system when it is excited by a step input.
Autoscale time	Automatically scales the x-axis on the Step Response graph.
Stable/Unstable	Indicates whether the resulting closed-loop system with the controller that this step creates is stable.
Model Input	Contains the following parameters: Plant (P)—Specifies the model to use as the plant (P) in the structure. Sensor (H)—Specifies the model in the feedback loop to use as the sensor (H) in the structure. Filter (F)—Specifies the model in the feedthrough with the feedback loop to use as the filter (F) in the structure. Feedback—Specifies the type of feedback loop.
Model Output	Contains the following options: Export Models—Contains the following parameters: Output controller (c)—Specifies that the step returns the final controller system. Closed loop (r-y)—Specifies that the step returns the complete closed-loop system. Control output (r-u)—Specifies that the step returns the equivalent system to analyze the control effort, or the signal applied to the input of the system. Loop transfer (CPH)—Specifies that the step returns the equivalent system for loop transfer in the series controller-plant-sensor. Plant sensitivity (dy-y)—Specifies that the step returns the equivalent system model for output sensitivity or the model from the output y against a disturbance in the output y. Output sensitivity (du-y)—Specifies that the step returns the equivalent system model for plant sensitivity or a variation of y against a disturbance in the input u. Sensor sensitivity (dh-y)—Specifies that the step returns the equivalent system model for sensor sensitivity or the model from the output y against a disturbance after the sensor H. Sampling time (s)—Defines the smallest sampling time used in the discrete models. If the system model is continuous or has a higher sampling rate, this step discretizes the model using zero-order-hold and the smallest sampling time.
Controller Synthesis	Contains the following parameters: Gain—Represents the proportional gain (Kc) of the controller. The default is 1. Integral (s)—Specifies the controller parameter (Ti) that adjusts the effect of the error integral term on the controller output. Derivative (s)—Specifies the controller parameter (Td) that adjusts the effect of the error derivative term on the controller output. HF Rolloff 1 (s)—Defines the cutoff frequency of a low frequency first order filter. If you place a checkmark in the Derivative (s) checkbox, the step automatically places a checkmark in the HF Rolloff 1 (s) checkbox. HF Rolloff 2 (s)—Defines the cutoff frequency of a second low frequency first order filter.

PID Synthesis Details

This step accepts four model inputs: plant, sensor, filter, and initial controller. Each input can be continuous or discrete and can have a unique sampling time. The PID Synthesis step determines the appropriate model representation for synthesis. For example, if all model inputs are continuous, the resulting synthesized PID controller also is continuous. If one or more input models is discrete, the resulting synthesized PID controller is a discrete controller sampled with the smallest sampling time of the discrete inputs.

Internally, all input models are resampled to use the smallest sampling time of the discrete input models before synthesis proceeds. All discretization is performed using the Zero-Order-Hold algorithm. If you want to use a different discretization method, use the Discretize Model step on all models before running the PID Synthesis step.