8.2 非线性方程式的实根

如果求根的方程式不为多项式的形态 就不能用 roots 函数。而这类的方策’h半是非线性方程式， 其函数形态变化很大。对于解这类方程式的根，可以用 fzero函数，它其实是用来找一函数 f(x) 的 x 值代入时，会使该函数值为零 (f(x)=0)；而这也就是根的特性，因此我们可以用 fzero求根。

要求任一方程式的根有三步骤：

1. 先定义方程式。要注意必须将方程式安排成 f(x)=0 的形态，例如一方程式为sin(x)=3， 则该方程式应表示为 f(x)=sin(x)-3。可以 m-file 定义方程式。
2. 代入适当范围的 x, y(x) 值，将该函数的分布图画出，藉以了解该方程式的「长相」。
3. 由图中决定y(x)在何处附近(x0)与 x 轴相交，以fzero的语法fzero('function',x0) 即可求出在 x0附近的根，其中 function 是先前已定义的函数名称。如果从函数分布图看出根不只一 个，则须再代入另一个在根附近的 x0，再求出下一个根。

以下分别介绍几数个方程式，来说明如何求解它们的根。

例一、方程式为

sin(x)=0

我们知道上式的根有 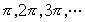，求根方式如下：

>> r=fzero('sin',3) % 因为sin(x)是内建函数，其名称为sin，因此无须定义它

r = % 选择 x=3 附近求根

3.1416

>> r=fzero('sin',6) % 选择 x=6 附近求根

r =

6.2832

例二、方程式为先前提到的 MATLAB 内建函数 humps，我们不须要知道这个方程式的形态为何，不过我们可以将它划出来，再找出根的位置。求根方式 如下：

>> x=linspace(-2,3);

>> y=humps(x);

>> plot(x,y), grid % 由图中可看出在0和1附近有二个根

>> r=fzero('humps',1.2)

r =

1.2995

例三、方程式为

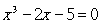
这个方程式其实是个多项式，我们说明除了用 roots 函数找出它的根外，也可以用这节介绍的方法求根，注意二者的解法及结果有所不同。求根方式如下：

% m-function, f_1.m

function y=f_1(x) % 定义 f_1.m 函数

y=x.^3-2*x-5;

>> x=linspace(-2,3);

>> y=f_1(x);

>> plot(x,y), grid % 由图中可看出在2和-1附近有二个根

>> r=fzero('f_1',2); % 决定在2附近的根

r =

2.0946

>> p=[1 0 -2 -5]

>> r=roots(p) % 以求解多项式根方式验证

r =

2.0946

-1.0473 + 1.1359i

-1.0473 - 1.1359i

例四、方程式为

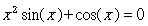
求根方式如下：

% m-function, f_2.m

function y=f_2(x) % 定义 f_2.m 函数

y=x.^2.*sin(x)+cos(x);

>> x=linspace(-3,3);

>> y=f_2(x);

>> plot(x,y), grid % 由图中可看出在-1和3附近有二个根

>> r=fzero('f_2',-1); % 决定在-1附近的根

r =

-0.8952

>> r=fzero('f_2',3); % 决定在3附近的根

r =

3.0333

例五、方程式为

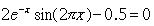
求根方式如下：

% m-function, f_3.m

function y=f_3(x) % 定义 f_3.m 函数

y=2*exp(-x).*sin(2*pi*x)-0.5;

>> x=0:0.1:2; y=f_3(x);

>> plot(x,y), grid % 由图中可看出在0,0.5和1附近有三个根

>> r=fzero('f_3',0) % 决定在0附近的根

r =

0.0420

>> r=fzero('f_3',0.5) % 决定在0.5附近的根

r =

0.4368

>> r=fzero('f_3',1) % 决定在1附近的根

r =

1.1435

上一页　下一页　讲义大纲