多项式的根

8.1 多项式的根

一个多项式视其阶数而定，它的根可以有一个到数个，可能为实数也可能是复数。要求一高阶多项式的根往往须借助数值方法，所幸MATLAB已将这些数值方法写成一函数roots(p)，我们只要输入多项式的各阶系数（以 p 代表）即可求解到对应的根。

>> p=[1 3 2];

>> r=roots(p)

r =

-2

-1

>> p=[1 -12 0 25 116]; % 注意二阶项系数为零须要输入，否则多项式的阶数就不对

>> r=roots(p) % 有实数根及复数根

r =

11.7473

2.7028

-1.2251 + 1.4672i

-1.2251 - 1.4672i

与 roots 相关的函数尚有 poly,real，这二个函数的用途是要验算求解的根展开能求得原多项式。例如有一个二次方程式的根为2, 1，则以下式计算原多项式

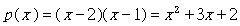
poly 函数就是在求出多项式的各阶系数，其语法为 poly(r)，其中 r 是代表根的阵列。而 real 则是用来去除因计算时产生的假虚部系数，为何会有此种情形请参考以下的例子。

>> r=[-2 1];

>> pp=poly(r) % pp=(x+2)(x-1)=x^2+3x+2

pp =

1 3 2

>> p=[1 -4 6 -4];

>> r=roots(p)

r =

2.0000 1.0000 + 1.0000i 1.0000 - 1.0000i

>> pp=poly(r) % 这个多项式的系数与原多项式 p 相同

pp =

1 -4 6 -4

>> pp=[1 7 12 9]; % 再看另一个多项式

>> r=roots(pp)

r =

-4.9395

-1.0303 + 0.8721i

-1.0303 - 0.8721i

>> pp=poly(r) % 注意因计算的误差会有假虚部产生

pp =

1.0000 7.0000 12.0000 9.0000 + 0.0000i

>> pp=real(pp) % 可以real将假虚部去除，将原多项式还原

pp =

1.0000 7.0000 12.0000 9.0000