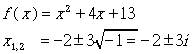复数

4.1.3 复数

要说明复数的运算，先从解以下的二次方程式的复数根谈起

上式的根有实部 (-2) 及虚部 (±3)，我们就这个复数的表示法来说明 MATLAB的复数功能。MATLAB 是以i或j字元来代表虚部，其它的复数相关函数有real, imag, conj, abs, angle等等，详见线上说明lookfor complex。如果复数表示为 x=a+bi

共轭复数 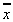=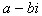, 复数大小r =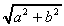, 复数向量的夹角 θ= tan^-1 (b/a)

复数实部a = r cosθ, 复数虚部b = r sinθ, 复数指数表示法 x=r eⁱ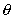

上述各函数对应MATLAB的复数指令为

a=real(x), b=imag(x), 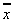=conj(x), r=abs(x), 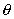=angle(x), x=r*exp(i*angle(x))

以下是几个复数表示式的例子：

>> x=1-2*i; % 注意是 2*i 不是 2i

>> real(x) % 列出实部

ans =

>> imag(x) % 列出虚部

ans =

-2

>> conj(x) % 计算共轭复数

ans =

1.0000 + 2.0000i

>> abs(x) % 计算复数的大小

ans =

2.2361

>> angle(x) % 计算复数向量的夹角（以径度表示）

ans =

-1.1071

>> a=1; b=4; c=13;

>> x1=(-b+sqrt(b^2-4*a*c))/(2*a) % 以解二次方程式根的公式计算复数根

x1 =

-2.0000 + 3.0000i

>> x2=(-b-sqrt(b^2-4*a*c))/(2*a)

x2 =

-2.0000 - 3.0000i

>> y=exp(i) % 以复数指数方式表示一个复数

y =

0.5403 + 0.8415i

>> y=exp(i*pi*0.75)

y =

-0.7071 + 0.7071i

和复数有关的图以极座标来表示会比一般的卡氏座标要合适，polar指令可以将数据以极座标方式加以绘图，其语法为 polar(theta,r)，(theta,r)分别代表极座标上的角度及半径值。以下的例子说明了 polar用法：

>> t=0:0.01:2*pi;

>> r=sin(2*t).*cos(2*t);

>> polar(t,r)

>> title('Polar plot of sin(2t)cos(2t)')

>> angle=0:2*pi/100:2*pi;

>> r=angle/(2*pi);

>> polar(angle,r)

>> title('Polar plot')

>> grid