---

假设 A为一个 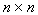矩阵，而 X 为一个有n列的栏向量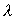，为一纯量。考虑以下的数学式

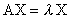
如果X由不为零的元素所组成，其中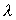要满足上式称为矩阵A的特徵值(eigenvalue)，而X称为矩阵A的特徵向量 (eigenvector)。特徵向量代表一个正规正交(orthonormal) 的向量组，所谓的正规正交向量，是指这向量与自身做 内积的值为一单位向量；在几何关系上是指二量相互垂直且此其内积值再做正规化(normalization)。

上式也可改写为

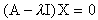
其中 I 为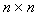单位矩阵。

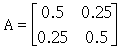
则eigenvalue可以用特徵方程式计算

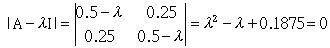
上述的二次方程式可求解二个根分别为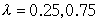，这二个值即为A的特徵值。而A的特徵向量求法如下 ，分别将任一特徵值代入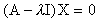。例如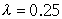

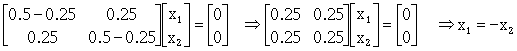
另一个特徵值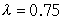代入，可以得到另一个特徵向量为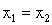。我们可找到无限多个向量，满足上述的 特徵向量，例如

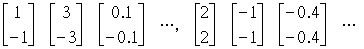
因此要得到唯一的特徵向量，即是正交(orthonormal)特徵向量组Q，利用其特性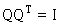

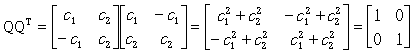
求解上式可得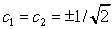。所以对应的正交特徵向量组Q为

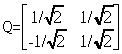
在上述例子中，矩阵A很简单大小为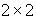，可以用手做演算。一但矩阵大小增加，以MATLAB内建函数做运 算，就很轻松。相关函数的语法为eig(A)，得到一栏向量代表A的特徵值；而[Q,d]=eig(A)，其中Q代表A的特徵 向量，d为一对角矩阵其元素代表A的特徵值。

在此示范上述例子

>> A = [0.5 0.25; 0.25 0.5];

>> [Q,d] = eig(A)

Q =

0.7071 0.7071

-0.7071 0.7071

d = % 注意在对角线上的值才是特徵值

0.2500 0

0 0.7500

>> Q*Q' % Q*Q'=I

ans=

1 0

0 1

>> A*Q(:,1); 0.25* Q(:,1) % 验证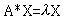，注意X=Q(:,1) 为第一个特徵向量

ans = % 为A*X的结果

0.1768

-0.1768

ans = % 为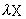的结果

0.1768

-0.1768

---

上一页　下一页　讲义大纲