矩阵分解 (decomposition, factorization)是多半将矩阵拆解为数个三角形矩阵(triangular matrix)，依使用目的的不同 ，可分为三种矩阵分解法：1)三角分解法 (Triangular Factorization)，2)QR 分解法 (QR Factorization)，3)奇异值分 解法 (Singular Value Decompostion)。

(1) 三角分解法

三角分解法是将原正方 (square) 矩阵分解成一个上三角形矩阵　或是排列(permuted) 的上三角形矩阵　和一个 下三角形矩阵，这样的分解法又称为LU分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程，求 反矩阵，和求解联立方程组。不过要注意这种分解法所得到的上下三角形矩阵并非唯一，还可找到数个不同 的一对上下三角形矩阵，此两三角形矩阵相乘也会得到原矩阵。

我们举以下二个矩阵为例：

利用三角分解法可将A和B二矩阵分别拆解为上下三角形矩阵

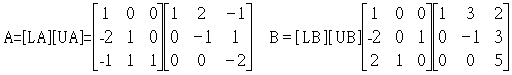
注意B分解的矩阵得到的第一个矩阵[LB]是排列的下三角形矩阵，如果第二、三列互换，则此变成完全的下 三角形矩阵。

以MATLAB函数计算上述的LU分解法，其语法为[L,U]=lu(A)，其中L代表下三角形矩阵U代表上三角形矩阵。 我们来看一个例子。

>> A = [1 2 -1, -2 -5 3; -1 -3 0]; B=[1 3 2; -2 -6 1; 2 5 7];

>> [L1,U1] = lu(A); [L2,U2] = lu(B);

>> L1; U1

L1 = % 注意这个矩阵L1和之前的[LA]不相同

-0.5 1 0

1 0 0

0.5 1 1

U1 = % 注意这个矩阵U1和之前的[UA]不相同

-2 -5 3

0 -0.5 0.5

0 0 -2

>> L2; U2

L2 = % 注意这个矩阵L2和之前的[LB]不相同

-0.5 0 1

1 0 0

-1 1 0

U2 = % 注意这个矩阵U2和之前的[UB]不相同

-2 -6 1

0 -1 8

0 0 2.5

(2) QR分解法

QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵。还记得先前我们介绍的正规正交矩阵Q满足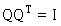的条件吗！所以称为QR分解法与此正规正交矩阵的通用符号Q有关。

MATLAB以qr函数来执行QR分解法， 其语法为[Q,R]=qr(A)，其中Q代表正规正交矩阵，而R代表上三角形矩 阵。此外，原矩阵A不必为正方矩阵；如果矩阵A大小为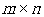，则矩阵Q大小为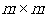，矩阵R大小为。
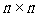(3) 奇异值分解法

奇异值分解 (sigular value decomposition,SVD) 是另一种正交矩阵分解法；SVD是最可靠的分解法，但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V代表二个相互正交矩阵，而S代表一对角矩阵。 和QR分解法相同者， 原矩阵A不必为正方矩阵。

使用SVD分解法的用途是解最小平方误差法和数据压缩。