---

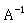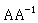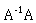一个正方矩阵A的反矩阵的定义是，所以此二矩阵相乘不论是或，结果皆为单位矩阵。但是一 矩阵如果是奇异(singular) 或是条件不足 (ill-conditioned)，其反矩阵并不存在。条件不足的矩阵与一组联立方程 组其中的方程式并不独立有关，而一矩阵的秩(rank) 即是代表矩阵中独立方程式个数。如果一矩阵的秩数和 其矩阵的列数相等，则此矩阵为非奇异且其反矩阵存在。

MATLAB的反矩阵函数和秩函数语法分别为inv(A), rank(A)，：例如：

>> A=[2 1; 4 3];

>> rank(A)

2 % 表示A秩数为2且等于矩阵的列数

>> inv(A) % 反矩阵

ans =

1.5000 -0.5000

-2.0000 1.0000

>> B=[2 1; 3 2; 4 5]; % B为奇异矩阵

>> rank(B)

ans =

2 % 表示B秩数为2，但是其列数为3

>> inv(B)

??? Error using ==> inv

Matrix must be square.

相信大家都会计算矩阵行列式的值，但是如一矩阵大小超过4以上，行列式值的计算就会繁复。MATLAB提供 计算行列式的函数，其语法为det(A)，例如：

>> A=[1 3 0; -1 5 2; 1 2 1];

>> det(A) % 矩阵之行列式值

ans =

10
沪p算就会繁复。MATLAB提供 计算行列式的函数，其语法为det(A)，例如：

>> A=[1 3 0; -1 5 2; 1 2 1];

>> det(A) % 矩阵之行列式值

ans =

10

---

上一页　下一页　讲义大纲