差分函数

9.3.2 差分函数

上述提及的后向差分式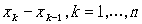，在 MATLAB 有对应的diff 函数来计算二相临点的差值，它的语法为 diff(x)，其中 x代表一组离散点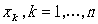。假设有x, y(x)的数据为

x=[1 3 5 7 9], y=[1 4 9 16 25]

则 diff(x)=[2 2 2 2], diff(y)=[3 5 7 9]，注意二者皆以后向差分计算且数据点只剩 4 个而不是5个。而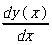的数值微分则为 dy=diff(y)./diff(x)。

因此要计算下列多项式在 [-4, 5] 区间的微分

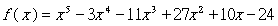
可依以下方式求解

>> x=linspace(-4,5); % 产生100个x的离散点

>> p=[1 -3 -11 27 10 -24];

>> f=polyval(p,x);

>> plot(x,f) % 将多项式函数绘图

>> title('Fifth-deg. equation')

>> dfb=diff(f)./diff(x); % 注意要分别计算diff(f)和diff(x)

>> xd=x(2:length(x)); % 注意只有99个df值，而且是对应x2,x3,...,x100的点

>> plot(xd,dfb ) % 将多项式的微分项绘图

>> title('Derivative of fifth-deg. equation')

假设我们要找出上述多项式的局部极值(local critical value)，可以利用局部极值所在点的微分为零，所以在这个点的左侧及右侧的二点微分值一定是一正一负，因此这二点的微分值相乘为负值，可针对此性质找出局部极值所在点。以原多项式的数据示范如下：

>> product=dfb(1:length(dfb)-1).*dfb(2:length(dfb)); % 注意二相临点值相乘的写法

>> crit=xd(find(product<0)) % 注意用到find指令

若上述多项式以中央差分方式计算其函数微分项，就不能以diff计算，而须自行计算如下：

>> num=f(3:length(f))-f(1:length(f)-2); % 注意中央差分是 f(k+1)-f(k-1)

>> deno=x(3:length(f))-x(1:length(f)-2); % 注意中央差分是 x(k+1)-x(k-1)

>> df_c=num./deno;

>> xd=x(2:length(x)-1); % xd的点数只有98个

>> plot(xd,df_c)

>> title('Derivative of fifth-deg. polynomial')

以下的例子是针对数据组为离散型态，要注意的是原数据所代表的函数分布并无明显的折角，但是它的一阶微分经数值微分计算后的微分函数分布却有极大的曲折变化。

>> x=0:0.1:1;

>> y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];

>> plot(x,y,'o',x,y)

>> title('y(x) data plot')

>> ylabel('y(x)'), xlabel('x')

>> dy=diff(y)./diff(x);

>> xd=x(1:length(x)-1);

>> plot(xd,dy)

>> title('Approximate derivative using diff')

>> ylabel('dy/dx'), xlabel('x')