---

和 polyfit有关的另一个函数是用来做多项式函数计算 polyval，由 polyfit 算出多项式的各个系数 (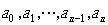)后，即可以 polyval 计算多项式的函数值。它的语法为polyval(coef,x)，其中 coef 是多项式的各个系数所构成的阵列，x则是要计算多项式值的x阵列。举一例说明

>> x=[0 1 2 3 4 5];

>> y=[0 20 60 68 77 110];

>> coef=polyfit(x,y,1); % 计算线性回归的各项系数

>> ybest=polyval(coef,x); % 直接以polyval计算多项式的数值

这个函数 polyval真是大大的好用，如果没有它的话，那我们要计算多项式的函数值还要费一番功夫。假设已有五阶的 多项式回归，要计算对应的多项式值，则须以下的步骤

>> coef=polyfit(x,y,5);

>> a0=coef(1);

>> a1=coef(2);

>> a2=coef(3);

>> a3=coef(4);

>> a4=coef(5);

>> a5=coef(6);

>> f=a0 + a1*x + a2*x.^2 + a3*x.^3 + a4*x.^4 + a5*x.^5;

我们接著示范从二阶到九阶的多项式回归的程式

>> x=[0 1 2 3 4 5];

>> y=[0 20 60 68 77 110];

>> newx=0:0.05:5; % 以新阵列形成更小增量以利回归计算及绘图

>> for n=2:9

>> f(:,n)=polyval(polyfit(x,y,n),newx)';

>> plot(newx,f(:,n),x,y,'o')

>> title(['Poly. regression, deg=',int2str(n)])

>> xlabel('Time'), ylabel('Temp'), grid

>> pause % 每次要暂停看清楚图再执行下一步骤

>> end

在上述的 title指令中我们示范了如何将一变数输入（n代表多项式的阶数），是利用int2str这个指令，它是用来 将一整数(integer) 转换成为一个字串 (string)，因为在title中只能以字串出现。此外在 title指令中尚须以 [ ] 将所有 叙述包括在内。类似的指令尚有 num2str 它是用来将实数转换成一字串。有关这几个新介绍的详细说明，请参 考 title, int2str, num2str 的线上说明。

---

上一页　下一页　讲义大纲