常微分方程式

11.2.2 常微分方程式

一阶常微分方程式 (first-order ordinary differential equation, ODE) 可写为

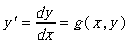
其中x为独立变数，而y是x的函数。上述的一阶常微分方程式的解是 y=f(x,y)可以满足y'=f'=g(x,y)。关于常微分方程式的解法已再第十章说明过，它还需要初始条件才能得到为一的解。

MATLAB解常微分方程式的语法是dsolve('equation','condition')，其中equation代表常微分方程式即y'=g(x,y)，且须以Dy代表一阶微分项y'　D2y代表二阶微分项y''　，condition则为初始条件。

假设有以下三个一阶常微分方程式和其初始条件

y'=3x², y(2)=0.5

y'=2^.x^.cos(y)², y(0)=0.25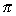

y'=3y+exp(2x), y(0)=3

对应上述常微分方程式的符号运算式为：

>>soln_1 = dsolve('Dy = 3*x^2','y(2)=0.5')

ans=

x^3-7.500000000000000

>>ezplot(soln_1,[2,4]) % 看看这个函数的长相

>>soln_2 = dsolve('Dy = 2*x*cos(y)^2','y(0) = pi/4')

ans=

atan(x^2+1)

>>soln_3 = dsolve('Dy = 3*y + exp(2*x)',' y(0) = 3')

ans=

-exp(2*x)+4*exp(3*x)