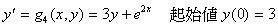10.2 阮奇-库达方法
阮奇-库达 (Runge-Kutta) 方法是最通用的解 ODE 的方法，它可以依计算精确度的要求有低阶到高阶的各个 计算式，举例来说，一阶阮奇-库达法为
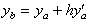
其实上式即是一阶的泰勒序数近似式，只不过令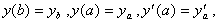 
。因为一阶阮奇-库达法 的精确度太低，所以在真正解ODE 时，最少须用二阶以上的方法。
MATLAB应用阮奇-库达法的函数有ode23,
ode45，其中ode23是同时以二阶及三阶阮奇-库达法求解，而ode45
则是以四阶及五阶阮奇-库达法求解。其语法为ode23('dy',x0,xn,y0)，其中
dy 为ODE中的等式右边的函数（如之 前介绍的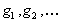
），x0,
xn 是要解ODE的区间 [x0, xn]
的二个端点，y0是起始值 (y0=y(x0))。而ode45的语法
与ode23相同。
先前的四个 ODE 的解法如下：
例一、要在区间 [2, 4] 解以下的 ODE：
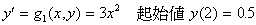
% m-function, g1.m
function dy=g1(x,y)
dy=3*x.^2;
>> [x,num_y]=ode23('g1',2,4,0.5);
>> anl_y=x.^3-7.5;
>> plot(x,num_y,x,anl_y,'o')
>> title('Solution of g1')
>> xlabel('x'), ylabel('y=f(x)'), grid
例二、要在区间 [0, 5] 解以下的 ODE：
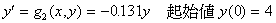
% m-function, g2.m
function dy=g2(x,y)
dy=-0.131*y;
>> [x,num_y]=ode23('g2',0,5,4);
>> anl_y=4*exp(-0.131*x);
>> plot(x,num_y,x,anl_y,'o')
>> title('Solution of g2')
>> xlabel('x'), ylabel('y=f(x)'), grid
例三、要在区间 [0, 2] 解以下的 ODE：
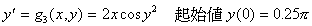
% m-function, g3.m
function dy=g3(x,y)
dy=2*x*cos(y)^2;
>> [x,num_y]=ode23('g3',0,2,pi/4);
>> anl_y=atan(x.*x+1);
>> plot(x,num_y,x,anl_y,'o')
>> title('Solution of g3')
>> xlabel('x'), ylabel('y=f(x)'), grid
例四、要在区间 [0, 3] 解以下的 ODE：
% m-function, g4.m
function dy=g4(x,y)
dy=3*y+exp(2*x);
>> [x,num_y]=ode23('g4',0,3,3);
>> anl_y=4*exp(3*x)-exp(2*x);
>> plot(x,num_y,x,anl_y,'o')
>> title('Solution of g4')
>> xlabel('x'), ylabel('y=f(x)'), grid
如果将上述方法改以 ode45 计算，你可能无法察觉出其与ode23的解之间的差异，那是因为我们选的 ODE 代表的函数分布变化平缓，所以高阶方法就显现不出其优点。不过以二者在计算的误差上做比较，ode45 的误差量级会比 ode23要小。以下是几个例子：
% m-function, g1.m
function dy=g1(x,y)
dy=3*x.^2;
% m-file, odes1.m
% Solve an ode using ode23 and ode45
clg
[x1,num_y1]=ode23('g1',2,4,0.5);
anl_y1=x1.^3-7.5;
error_1=abs(anl_y1-num_y1)./abs(anl_y1); % ode23 的计算误差
[x2,num_y2]=ode45('g1',2,4,0.5);
anl_y2=x2.^3-7.5; % 注意 x2 个数与 x1 不一定相同
error_2=abs(anl_y2-num_y2)./abs(anl_y2); %
ode45 的计算误差
hold on
subplot(2,2,1)
plot(x1,num_y1,x1,anl_y1,'o')
title('ODE23 solution'), ylabel('y')
subplot(2,2,2)
plot(x1,error_y1) % 注意二种方法的误差
title('ODE23 error'), ylabel('y') % ode23 的误差的量级为 1.e-16
subplot(2,2,3)
plot(x2,num_y2,x2,anl_y2,'o')
title('ODE45 solution'), ylabel('y')
subplot(2,2,4)
plot(x1,error_y2)
title('ODE45 error'), ylabel('y') % ode45 的解没有误差
hold off
另一个例子：
% m-function, g5.m
function dy=g5(x,y)
dy=-y+2*cos(x);
% m-file, odes1.m
% Solve an ode using ode23 and ode45
clg
[x1,num_y1]=ode23('g5',0,5,1);
anl_y1=sin(x1)+cos(x1);
error_1=abs(anl_y1-num_y1)./abs(anl_y1);
[x2,num_y2]=ode45('g5',0,5,1);
anl_y2=sin(x2)+cos(x2);
error_2=abs(anl_y2-num_y2)./abs(anl_y2);
hold on
subplot(2,2,1)
plot(x1,num_y1,x1,anl_y1,'o')
title('ODE23 solution'), ylabel('y')
subplot(2,2,2)
plot(x1,error_y1) % 注意二种方法的误差
title('ODE23 error'), ylabel('y') % ode23 的误差的量级为 1.e-4
subplot(2,2,3)
plot(x2,num_y2,x2,anl_y2,'o')
title('ODE45 solution'), ylabel('y')
subplot(2,2,4)
plot(x1,error_y2)
title('ODE45 error'), ylabel('y') % ode45 的误差的量级为 1.e-6
hold off
上一页 下一页 讲义大纲