10.1 微分方程式
一个一阶常微分方程式 (ordinary differential equation, ODE) 可以下式表示
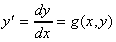
其中x 为独立变数而 y 是 x 的函数,我们就是要求解什么函数 y(x) 能满足上述 ODE。以下有几个一阶 ODE 的例子:
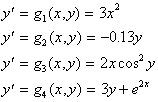
除了上述的已知ODE外,还须有起始条件y0=y(x0)才能解方程式,即是在x=x0时,y(x)=y0。上述各个方程式 的解析解 (analytical solution) 如下:
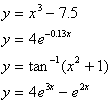
以数值方法求解上述的 ODE 的问题,可以转换为在已知 y(a) 的函数值而要计算y(b),依据泰勒序数对 y(b) 做展开
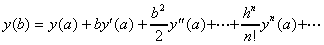
其中 b=a+h。一个一阶的泰勒序数近似式为
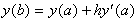
而二阶的泰勒序数近似式为
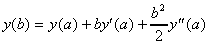
MATLAB 所依据解ODE 的数值方法就是利用像上述的二阶及更高阶的三、四、五阶泰勒序数近似式来计算
f(b)。



上一页 下一页 讲义大纲