 |
 |
 |
 |
World to Screen TransformationAuthor Ernie Wright This page tells you how to convert from LightWave's world (x, y, z) coordinates to pixel coordinates in the rendered image. It relates parameters available from the LightWave plug-in API to components of the synthetic camera model, a method for defining the position of a virtual camera in 3D space and determining what it can see.
The unit vectors u, v and n correspond to the axes of the UVN system. Position vector r is the origin of UVN, sometimes called the view reference point, or VRP. Given these vectors and the eye distance e, we can express the world to image space transformation as a single 4 x 4 matrix M, |
|||||||||||||||||
|
|||||||||||||||||
| The upper left 3 x 3 submatrix rotates the world into the UVN orientation
and contains the components of u, v and n. The bottom row translates
the origin along r', derived from r by r' = (- r · u, - r · v, - r · n) The rightmost column contains the perspective foreshortening terms. To transform the point p, multiply its homogeneous position vector (px, py, pz, 1) by matrix M. The result is the transformed point in viewing coordinates. For pixel coordinates, you need to divide by the width and height of a pixel. Doing It from a Plug-in In your activation function, get the globals you'll need. LWItemInfo *lwi; LWCameraInfo *lwc; LWSceneInfo *lws; lwi = global( LWITEMINFO_GLOBAL, GFUSE_TRANSIENT ); lwc = global( LWCAMERAINFO_GLOBAL, GFUSE_TRANSIENT ); lws = global( LWSCENEINFO_GLOBAL, GFUSE_TRANSIENT ); if ( !lwi || !lwc || !lws ) return AFUNC_BADGLOBAL; When you're ready to do the transformation, get the camera's RIGHT, UP, FORWARD and W_POSITION vectors, and the camera zoom factor. These correspond to u, v, n, r (sort of) and e. LWItemID id; LWTime lwtime; double u[ 3 ], v[ 3 ], n[ 3 ], r[ 3 ], e; id = lws->renderCamera( lwtime ); lwi->param( id, LWIP_RIGHT, lwtime, u ); lwi->param( id, LWIP_UP, lwtime, v ); lwi->param( id, LWIP_FORWARD, lwtime, n ); lwi->param( id, LWIP_W_POSITION, lwtime, r ); e = -lwc->zoomFactor( id, lwtime ); Fill in the transformation matrix. typedef double MAT4[ 4 ][ 4 ]; MAT4 t; t[ 0 ][ 0 ] = u[ 0 ]; t[ 0 ][ 1 ] = v[ 0 ]; t[ 0 ][ 2 ] = n[ 0 ]; t[ 1 ][ 0 ] = u[ 1 ]; t[ 1 ][ 1 ] = v[ 1 ]; t[ 1 ][ 2 ] = n[ 1 ]; t[ 2 ][ 0 ] = u[ 2 ]; t[ 2 ][ 1 ] = v[ 2 ]; t[ 2 ][ 2 ] = n[ 2 ]; t[ 3 ][ 0 ] = -dot( r, u ); t[ 3 ][ 1 ] = -dot( r, v ); t[ 3 ][ 2 ] = -dot( r, n ) + e; t[ 0 ][ 3 ] = -n[ 0 ] / e; t[ 1 ][ 3 ] = -n[ 1 ] / e; t[ 2 ][ 3 ] = -n[ 2 ] / e; t[ 3 ][ 3 ] = 1.0 - t[ 3 ][ 2 ] / e; Multiply the point by the matrix. double pt[ 3 ], tpt[ 3 ], w; w = transform( pt, t, tpt ); At this point, you'll probably want to test whether the transformed point is actually visible in the image. It might be behind the camera, or in front of it but outside the boundaries of the viewport. The z coordinate returned by the transformation, however, is the pseudodepth, which has desireable mathematical properties but isn't very useful for visibility testing in LightWave. We calculate the true z distance (the perpendicular distance from the camera plane) instead, using the homogeneous coordinate w returned by our transform function. zdist is the value that would be in the z-buffer for the point. double zdist, frameAspect;
zdist = w * tpt.z - e;
if ( zdist <= 0 ) {
// the point is behind the camera ...
frameAspect = lws->pixelAspect * lws->frameWidth / lws->frameHeight;
if (( fabs( tpt.y ) > 1 ) || ( fabs( tpt.x ) > frameAspect )) {
// the point is outside the image rectangle ...
Finally, convert from meters (on the projection plane) to pixels. double s, x, y; s = lws->frameHeight * 0.5; y = s - tpt.y * s; x = lws->frameWidth * 0.5 + tpt.x * s / lws->pixelAspect; The transform function looks like double transform( double pt[ 3 ], MAT4 t, double tpt[ 3 ] )
{
double w;
tpt[ 0 ] = pt[ 0 ] * t[ 0 ][ 0 ]
+ pt[ 1 ] * t[ 1 ][ 0 ]
+ pt[ 2 ] * t[ 2 ][ 0 ] + t[ 3 ][ 0 ];
tpt[ 1 ] = pt[ 0 ] * t[ 0 ][ 1 ]
+ pt[ 1 ] * t[ 1 ][ 1 ]
+ pt[ 2 ] * t[ 2 ][ 1 ] + t[ 3 ][ 1 ];
tpt[ 2 ] = pt[ 0 ] * t[ 0 ][ 2 ]
+ pt[ 1 ] * t[ 1 ][ 2 ]
+ pt[ 2 ] * t[ 2 ][ 2 ] + t[ 3 ][ 2 ];
w = pt[ 0 ] * t[ 0 ][ 3 ]
+ pt[ 1 ] * t[ 1 ][ 3 ]
+ pt[ 2 ] * t[ 2 ][ 3 ] + t[ 3 ][ 3 ];
if ( w != 0 ) {
tpt[ 0 ] /= w;
tpt[ 1 ] /= w;
tpt[ 2 ] /= w;
}
return w;
}
and dot is just double dot( double a[ 3 ], double b[ 3 ] )
{
return ( a[ 0 ] * b[ 0 ] + a[ 1 ] * b[ 1 ] + a[ 2 ] * b[ 2 ] );
}
|
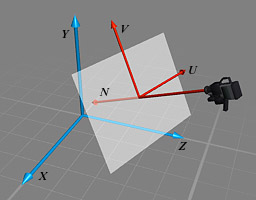 Pixels lie on the
view plane in the camera's UVN coordinate system. The camera itself is set back from the
view plane by an amount called the eye distance that controls the perspective
foreshortening.
Pixels lie on the
view plane in the camera's UVN coordinate system. The camera itself is set back from the
view plane by an amount called the eye distance that controls the perspective
foreshortening.