Rounding

The Clipper Library

Rounding

By requiring integer coordinates for all polygon vertices, the Clipper Library has been able to avoid problems of numerical robustness that otherwise plague geometric computations. Nevertheless, rounding coordinates to integers causes other problems, and these are discussed below.

It is important to stress at the outset that rounding causes some unavoidable imprecision by moving vertices fractions of a unit away from their 'true' positions. Fortunately rounding imprecision can be managed effectively by appropriate scaling.

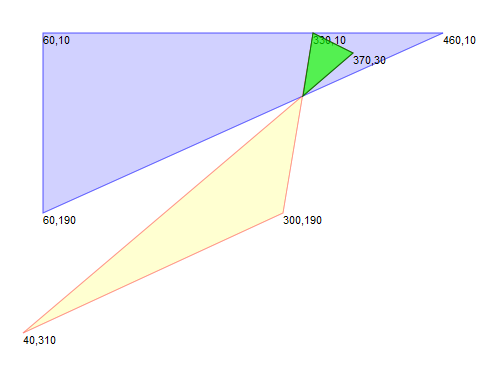
Nevertheless inappropriate scaling can deliver undesirable and perhaps unexpected solutons as demonstrated by the first example on the right. The image shows two polygons (triangles) being merged with a 'union' operation. The region shaded green represents the 'merged' polygon returned by Clipper. It's evident that the bottom-left polygon from the input is missing from the result.

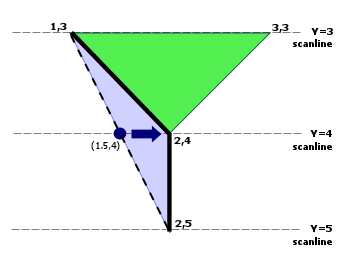
This is perhaps best explained by a very simple overview of how the clipping algorithm is implemented. Imaginary horizontal lines (called scanlines) pass through each and every vertex in the supplied set of polygons (ie both subject and clip polygons). The regions between adjacent scanlines are called scanbeams. Scanbeams are processed in order, starting with the bottom-most scanbeam and proceeding to the top-most. For each scanbeam there is a set of 'active' edges, that is those edges that pass through that scanbeam. The relative positions of active edges at both the bottom and top of a given scanbeam are used to determine the locations of intersections within a scanbeam. To preserve numerical robustness it's necessary to use the rounded coordinates of each edge at each scanline. This rounding effectively causes edges to deviate fractions of a unit horizontally where they cross each scanline.

In the image on the right the edge (2,5) -> (1,3) deviates from its true position at (1.5,4) to (2,4) at scanline Y=4. This edge deviation reduces the bottom-left polygon's area to zero and as a consequence it is discarded.

If the polygon coordinates of these 2 triangles had been scaled up by even just a factor of 2, ie {(2,6), (4,8), (4,10)} and {(2,6), (6,6), (4,8)}, the union operation would have returned a polygon that correctly covers both triangles.

Greater precision can always be achieved by scaling (or increased scaling) of polygon coordinates. The Clipper library accepts integer coordinate values up to ±0x3FFFFFFFFFFFFFFF (± 4.6e+18) in order to accommodate very high degrees of precision.

This second clipping example shows another complication of rounding - tiny self-intersection artefacts. Even though polygon vertices passed to Clipper objects have integer coordinates, their edges commonly intesect with other edges at fractional coordinates. These intersection points (that form vertices in the solution polygons) must have their coordinates rounded to integers.

In the unscaled image on the left (where one unit equals one pixel), the area of intersection of 2 polygons has been highlighted in bright green.

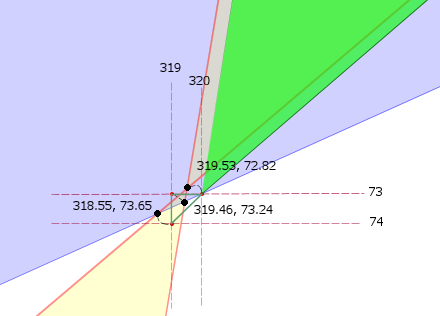
A 30X 'close up' of the lower points of intersection of these same 2 polygons shows the presence of a tiny self-intersecting artefact. The three 'black dots' highlight the actual points of intersection (with their fractional coordinates displayed). The smaller 'red dots' show where these points of intersection are located once rounding is applied. With a little care you can see that rounding reverses the orientation of these vertices and causes a tiny self-intersecting artefact.

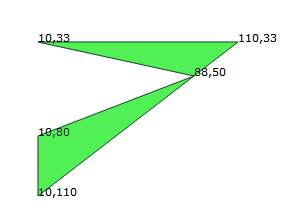
In this final example, the single polygon on the left also has a tiny self-intersection. However, due to the way Clipper uses rounding (as very briefly outlined above), the vertex (88,50) is seen to simply 'touch' rather than cross over (by a fraction of a unit) the right edge of the polygon. Consequently a union operation by Clipper on this polygon will return this same polygon unchanged (ie without removing the tiny self-intersection).

previous page start next page