MATLAB 另外提供二种积分函数，它们分别是辛普森法 quad 和牛顿-康兹法 quad8。三种方法的精确度由低 而高，分别为 trapz, quad, quad8。

由于这二种方法依据的积分法不同于梯形法，因此它们的语法就和 trapz 不同；其语法为 quad('function',a,b) （quad8语法相同），其中function是一已定义函数的名称（如sin, cos, sqrt, log 等），而 a, b是积分的下限和 上限。和 trapz比较，quad, quad8不同之处在于这二者类似解析式的积分式，只须设定上下限及定义要积分 的函数；而 trapz则是针对离散点型态的数据做积分。

我们看一简单积分式

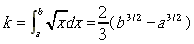
以下为 MATLAB 的程式

>> a=0; b=0.5;

>> kq=quad('sqrt',a,b)

kq =

0.2357

>> kq8=quad8('sqrt',a,b)

kq8 =

0.2357

再来看一个较复杂的积分式

>> x=-1:0.17:2;

>> y=humps(x);

>> area=trapz(x,y)

area =

25.9174

>> x=-1:0.07:2;

>> y=humps(x);

>> area=trapz(x,y)

area =

26.6243

>> area=quad('hump',-1,2)

area =

26.3450

>> area=quad8('hump',-1,2)

area =

26.3450