利用矩阵解法

6.1 利用矩阵解法

假设一组联立线性方程式为

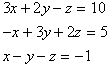
我们习惯将上组方程式以矩阵方式表示如下

AX=B

其中 A 为等式左边各方程式的系数项，X 为欲求解的未知项，B 代表等式右边之已知项

要解上述的联立方程式，我们可以利用在第六章介绍的矩阵左除 \ 做运算，即是 X=A\B。

如果将原方程式改写成 XA=B，且令 X, A 和 B 分别为

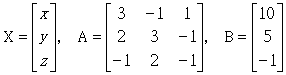
注意上式的 X, B 已改写成列向量，A其实是前一个方程式中 A 的转置矩阵。上式的 X 可以矩阵右除 / 求解，即是 X=B/A。

若以反矩阵运算求解 AX=B, X=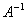B，即是 X=inv(A)*B，或是改写成 XA=B, X=B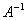，即是 X=B*inv(A)。

我们直接以下面的例子来说明这三个运算的用法：

>> A=[3 2 -1; -1 3 2; 1 -1 -1]; % 将等式的左边系数键入

>> B=[10 5 -1]'; % 将等式右边之已知项键入，B要做转置

>> X=A\B % 先以左除运算求解

X = % 注意X为行向量

-2

>> C=A*X % 验算解是否正确

C = % C=B

-1

>> A=A'; % 将A先做转置

>> B=[10 5 -1];

>> X=B/A % 以右除运算求解的结果亦同

X = % 注意X为列向量

10 5 -1

>> X=B*inv(A); % 也可以反矩阵运算求解