高阶常微分方程式

10.4 高阶常微分方程式

一个高阶常微分方程式可以利用变数改变(change of variables) 方式改写成个一组联立的一阶常微分方程式。例如以下的 n 阶方程式

我们先定义 n 个新的变数来取代上式中的

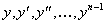
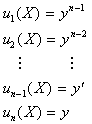
将上述的新变数代入原 ODE，连同这些新变数即构成一组联立的一阶常微分方程式

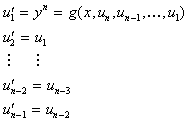
我们接者以一个二阶 ODE 为例说明上述的过程

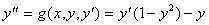
我们须要定义

将上述的二变数代入原 ODE，即构成一组联立的一阶常微分方程式

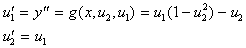
以下即是上述二阶 ODE 的解法：

function u_prime =eqns2(x,u)

u_prime(1) = u(1)*(1-u(2)^2) - u(2);

u_prime(2) = u(1);

initial = [0 0.25];

[x,num_y] = ode23('eqns2',0,20,initial);

subplot(2,1,1), plot(x,num_y(:,1))

title('1st derivative of y'), xlabel('x'), grid

subplot(2,1,2), plot(x,num_y(:,2))

title('y'), xlabel('x'), grid