Mesure de la fréquence analogique
Certains périphériques peuvent mesurer la fréquence analogique directement en utilisant un circuit de fréquence en tension. Toutefois, la plupart des périphériques mesurent uniquement la tension et il vous faudra utiliser des algorithmes logiciels en vue de convertir ces mesures en fréquence.
Les périphériques qui mesurent la fréquence analogique, comme les périphériques DSA et le SCXI-1126, possèdent un circuit capable de produire des déclenchements de la même fréquence que celle du signal mesuré. Chaque fois que le signal passe du niveau de seuil moins l'hystérésis au niveau de seuil, un déclenchement a lieu. Un générateur d'impulsions utilise ces déclenchements et produit une impulsion à chaque cycle de fréquence. La plage de fréquence en entrée définit la largeur de cette impulsion. Au fur et à mesure que la gamme de fréquences d'entrée s'accroît, la largeur de l'impulsion diminue. Ce train d'impulsions est ensuite converti en un signal CC dont le niveau est proportionnel au rapport cyclique du train d'impulsions. Le rapport cyclique correspond à une fraction de période du train d'impulsions au moment où l'impulsion a lieu. Le signal CC a une tension qui est proportionnelle à la fréquence d'entrée et qui peut donc être mis à l'échelle de cette valeur de fréquence.
Pour les périphériques qui ne peuvent pas mesurer la fréquence directement, vous devez utiliser les algorithmes logiciels, comme la transformée de Fourier rapide (FFT), pour convertir une tension en fréquence. Les systèmes de développement complet et de développement professionnel de LabVIEW comprennent des VIs d'analyse avancés capables de gérer ces transformations. Le système de développement complet LabWindows™/CVI™ comprend aussi des fonctions d'analyse avancées conçues pour vous aider à mesurer la fréquence analogique. Vous devez échantillonner à une fréquence au moins deux fois supérieure à celle de la composante ayant la plus haute fréquence dans le signal que vous acquérez, que vous utilisiez des fonctions ou des VIs existants ou que vous en créiez de nouveaux.
Fréquence analogique, fréquence d'échantillonnage et le théorème de Nyquist
Le théorème de Nyquist démontre que la plus haute fréquence que vous pouvez représenter avec précision correspond à la moitié de la fréquence d'échantillonnage. Par exemple, pour mesurer la fréquence d'un signal de 100 Hz, il vous faut une fréquence d'échantillonnage d'au moins 200 É/s. Dans la pratique, vous devriez utiliser des fréquences d'échantillonnage 5 à 10 fois supérieures aux fréquences attendues afin d'améliorer la précision des mesures.
Outre la fréquence d'échantillonnage, vous devez déterminer le nombre d'échantillons à acquérir. Vous devez échantillonner un minimum de trois cycles du signal analogique. Par exemple, vous devez acquérir au moins 15 échantillons, ou points, si vous utilisez une fréquence d'échantillonnage de 500 Éch/s pour mesurer la fréquence d'un signal de 100 Hz. Comme la fréquence d'échantillonnage que vous utilisez est environ cinq fois plus rapide que la fréquence du signal, vous échantillonnez environ cinq points par cycle de signal. Vous avez besoin des données de trois cycles, donc 5 points x 3 cycles = 15 points. Dans la pratique, toutefois, comme il vous faut acquérir 10 cycles ou plus afin d'optimise la précision des mesures, vous devriez acquérir au moins 50 échantillons.
Le nombre de points recueillis détermine le nombre d'intervalles de fréquence dans lequel se situent les échantillons. La taille de chaque intervalle est égale à la fréquence d'échantillonnage divisée par le nombre de points que vous recueillez. Par exemple, si vous échantillonnez à une fréquence de 500 Éch/s et que vous acquérez 100 points, les intervalles sont de 5 Hz chacun.
La fréquence de Nyquist correspond à la bande passante du signal échantillonné et équivaut à la moitié de la fréquence d'échantillonnage. Les composantes fréquentielles inférieures à la fréquence de Nyquist apparaissent normalement. Les composantes fréquentielles supérieures à la fréquence de Nyquist apparaissent avec un repliement compris entre 0 et la fréquence de Nyquist. La composante repliée est la valeur absolue de la différence entre la composante réelle et le multiple entier le plus proche de la fréquence d'échantillonnage. Par exemple, si vous avez un signal avec une composante fréquentielle à 800 Hz et que vous échantillonnez à une fréquence de 500 Éch/s, cette composante apparaît repliée à 200 Hz car |800–(2 x 500)| = 200(Hz).
Une façon d'éliminer les composantes repliées consiste à utiliser un filtre matériel analogique avant de numériser et d'analyser les informations de fréquence. Si vous voulez effectuer tout le filtrage dans le logiciel, vous devez d'abord échantillonner à une fréquence suffisamment rapide pour représenter correctement la plus haute composante fréquentielle du signal. Par exemple, si la plus haute composante fréquentielle est à 800 Hz, la fréquence d'échantillonnage minimale est de 1600 Hz mais vous devez échantillonner à une fréquence 5 à 10 plus rapide que 800 Hz. Si la fréquence que vous souhaitez mesurer se situe aux environs de 100 Hz, vous pouvez utiliser un filtre passe-bas de Butterworth avec une fréquence de coupure (fc) de 250 Hz afin de filtrer les fréquences supérieures à 250 Hz et laisser passer les fréquences inférieures à 250 Hz.
 |
Remarque Des filtres de Butterworth sont inclus dans les systèmes de développement complet et de développement professionnel de LabVIEW. |
Mesure de la fréquence au moyen de filtres
La figure suivante représente un filtre passe-bas.
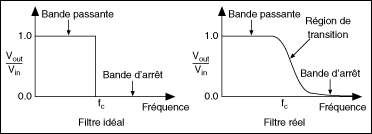
Filtre passe-bas
Le filtre idéal dans la figure est optimal. Toutes les fréquences supérieures à la fréquence de Nyquist sont rejetées. Le filtre réel dans la figure correspond à ce que vous serez probablement en mesure d'accomplir avec le filtre de Butterworth. La bande passante se situe à l'emplacement où Vout/Vin est proche de 1. La bande d'arrêt a lieu là où Vout/Vin est proche de 0. Les fréquences s'atténuent progressivement sur la zone de transition entre 1 et 0.