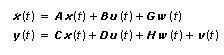Mathematical Model Definitions (Control Design and Simulation Module)

The LabVIEW Control Design and Simulation Module provides tools to study the dynamics of systems described by linear time-invariant (LTI) continuous and discrete models. You can create deterministic state-space, transfer function, and zero-pole-gain models. You also can create stochastic state-space models and the second-order statistics noise models. You can use these forms to describe both single-input single-output (SISO) and multiple-input multiple-output (MIMO) systems.

Continuous transfer function and zero-pole-gain models use the s variable to define time, whereas discrete transfer function and zero-pole-gain models use the z variable to define time. Continuous state-space models use the t variable to define time, whereas discrete state-space models use the k variable to define time.

Deterministic State-Space Model

Continuous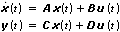
Discrete	x(k + 1) = Ax(k) + Bu(k)
	y(k) = Cx(k) + Du(k)

Stochastic State-Space Model

Continuous
Discrete	x(k + 1) = Ax(k) + Bu(k) + Gw(k)
	y(k) = Cx(k) + Du(k) + Hw(k) + v(k)
Second-Order Statistics Noise Model	Q = E{w . wT} – E{w} . ET{w}
	R = E{v . vT} – E{v} . ET{v}
	N = E{w . vT} – E{w} . ET{v}

where	t is continuous time.
	k is the model sampling time multiplied by the discrete time step, where the discrete time step equals 0, 1, 2, …
	x is the model state vector.
	u is the model input vector.
	y is the model output vector.
	w is the process noise vector.
	v is the measurement noise vector.
	A is an n × n state matrix of the given model.
	B is an n × m input matrix of the given model.
	C is an r × n output matrix of the given model.
	D is an r × m direct transmission matrix of the given model.
	n is the number of model states.
	m is the number of model inputs.
	r is the number of model outputs.
	G is a matrix relating w to the model states.
	H is a matrix relating w to the model outputs.
	Q is the auto-covariance matrix of w.
	R is the auto-covariance matrix of v.
	N is the cross-covariance matrix between w and v.
	E{} denotes the expected value or the mean of the enclosed term(s).

Transfer Function Model

	SISO	MIMO
Continuous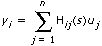
Discrete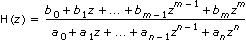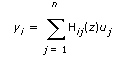

Zero-Pole-Gain Model

	SISO	MIMO
Continuous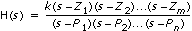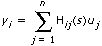
Discrete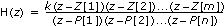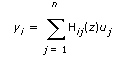

where	s is the Laplace variable and continuous time
	z is discrete time
	m is the order of the numerator polynomial function
	n is the order of the denominator polynomial function
	bm are the coefficients of the numerator polynomial function
	an are the coefficients of the denominator polynomial function
	Zm are the locations of the model zeros
	Pn are the locations of the model poles
	k is the gain of the model
	Hij is the transfer function or zero-pole-gain equation at the ith input and jth output of a MIMO model